統計学と機械学習におけるマルチコ(多重共線性)に対する考えの相違
- 2019.05.27
- 統計解析
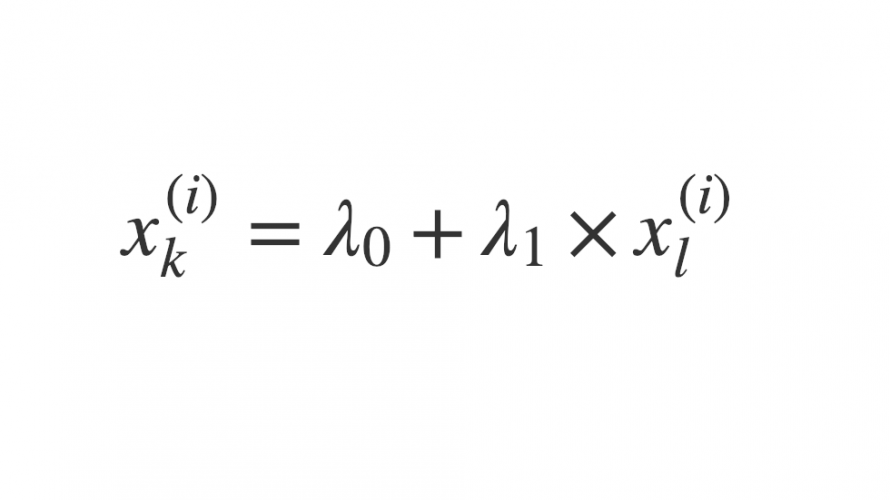
先日、デスマーチの末なんとか機械学習案件のリリースに漕ぎ着けました。
今回の案件に関わらないですが、要件や仕様はしっかり明文化しておくべきですね。
後から(特にリリース間近になって)言った言わないの議論になるのは双方にとってあまり気持ちのいいものではありません。
些細な仕様変更のため口頭で合意した内容でも、しっかりと資料化しておくことの重要さを再認識しました。
さて、今回はマルチコ(多重共線性)について投稿します。
クライアント先で多変量解析をしているときにこの話題が出たので、いろいろと調べてみました。
大学では統計学視点でのマルチコを若干勉強したのですが、この機会に再度勉強し直してみたのでまとめます。
マルチコ(多重共線性)とは
マルチコとは、重回帰モデルにおいて説明変数間に強い相関がある事象のことをいいます。
マルチコはmulti-colinearlity(マルチ-コリニアリティ)の略称で、完全に和製な呼び方なので海外の人にマルチコと言っても通じません。
さて、マルチコには2つバリエーションがあります。
Structural multicollinearity
交互作用項やべき乗項など、既存の説明変数から新しい説明変数を生成することによって生じるマルチコです。
例えば、既存の説明変数\( x \)から \( x^2 \)を作った場合、\( x \)と \( x^2 \)には強い相関関係が生じます。
(\( x \)が大きいほど \( x^2 \)も大きくなるので相関があります)
Data-based multicollinearity
観測されたデータに存在している説明変数間で生じるマルチコです。
例えば、年齢と社歴を説明変数に、年収を目的変数とする回帰モデルを構築した場合を考えます。
この場合、説明変数である年齢と社歴には強い相関関係があります。
(年齢が高いほど社歴は高く、逆もまたしかりです。)
Structural multicollinearityは自ら説明変数を操作することで生じるためコントロールが容易ですが、Data-based multicollinearityは観測データにマルチコが含まれているため注意が必要です。
数式で理解するマルチコ
さて、ここではマルチコだと何が良くないのかを説明します。
以下の線形回帰モデルを考えましょう。
$$ y^{(i)} = \beta_0 + \beta_1 x^{(i)}_{1} +\beta_2 x^{(i)}_{2} \cdots + \beta_n x^{(i)}_{n} + \epsilon $$
\( y^{(i)} \)は\( i \)番目の\( y \)の要素、\( x^{(i)}_{n} \)は\( i \)番目の\( X_{n} \)の要素であり、\( \beta \)は回帰係数です。
パラメータ\( \beta \)は正規方程式によって以下のように計算できます。
(正規方程式については説明しませんが、重回帰のパラメータを行列計算でスマートに解ける方程式と思ってもらえればOKです。)
$$ \hat{\beta} = \left ( X^T X \right)^{-1}X^T y $$
ここで、説明変数間に強い相関関係がある場合、以下のようにある説明変数が他の説明変数で表現できることになります。
$$ x_{k}^{(i)} = \lambda_0 + \lambda_1 \times x_{l}^{(i)} $$
このとき、\( X := (x_1,x_2,\dots,x_n) \) の各説明変数は一次独立ではなくなる、すなわち、\( X \)がフルランクではなくなるために逆行列を計算できません。
したがって、パラメータ\( \hat{\beta} \)も算出できなくなるのです。
(実際は擬似逆行列を計算することで解を得ますが、非常に不安定な数値となります)
マルチコの捉え方の違い
このように回帰モデルの構築時には厄介なマルチコですが、統計学、機械学習観点では捉え方が異なります。
統計学におけるマルチコ
統計学観点では、マルチコは放置してはいけない事象になります。
統計学における回帰分析では、目的変数に対する説明変数の影響度を理解することをゴールにしています。
しかし、説明変数間に強い相関関係がある場合にはマルチコが発生し、マルチコが起きている説明変数の回帰係数は解釈不明な数値を示すことになります。
統計学のゴールから言えば、回帰係数からどの説明変数が目的変数に寄与するかを正確に判断することが重要なので、マルチコは避けなければいけません。
機械学習におけるマルチコ
一方、機械学習は統計学とは異なり、モデルの予測精度に関心があり、説明変数間の影響度合には注意を払いません。
実際、マルチコはモデルの説明力を低下させるものの、予測精度に影響を与えないとも言われています。
(ただし、未知のデータに対する予測精度は悪くなる可能性が高いです。)
また、機械学習アルゴリズムの多く(特に決定木やLASSOなど)は内部的に特徴量に対して正則化or特徴選択を施しているため回帰係数が安定します。
こういったこともあって、機械学習はマルチコを特段意識する必要がないと言えます。
まとめ
以上より、マルチコの捉え方は統計学、機械学習で異なります。
また、昨今の機械学習ブームによって、予測精度のみを求めている(つまりモデルがどう特徴量を選んだのかを気にしない)人が増えてきた印象があります。
しかし、データサイエンティストとしてデータ・ドリブンなビジネス推進を目指すのであれば、構築したモデルの説明力にも気を払う必要があると思います。
人を動かせるのは簡潔でわかりやすいモデルです。
今一度、統計学に立ち返ってみるのも大事だなと思いました。
参考
マルチコを理解するのに使ったページを紹介します。
- 前の記事

雪崩から生還〜山岳事故に巻き込まれるリスクを考える 2019.05.19
- 次の記事
Tableauでカレンダー形式のダッシュボードを作成する方法 2019.07.23