モンテカルロ法による円周率のシミュレーション

暇つぶしがてら、モンテカルロ法で円周率をシミュレーションしてみました。

円周率という神秘的で秩序だった定数を、乱数により近似するというアイデアの実装はなかなか楽しいものでした。
（別に目新しい方法ではないですけどね。）

モンテカルロ法とは

モンテカルロ法とは、乱数を用いたシミュレーションのことです。

例えば、サイコロの出る目が1/6（等確率）であることの証明を考えます。

理論的にサイコロの出る目が等確率であることを証明するには、少なくとも以下の証明が必要でしょう。

1. サイコロの各面に一切の歪みがないこと
2. サイコロの重心が出目の彫に応じた位置になっていること
3. サイコロを投げる場が水平で、かつ歪みがないこと

などなど、物理的な検証も必要なので面倒ですね。

しかし、実際に数万回サイコロを振ってみて、各目が1/6に近い確率で出ることが判明すれば、サイコロの出目が等確率であることの立派な証明となります。

理論を知らなくても、力業でシミュレーションすることで検証できるのがモンテカルロ法の強みと言えます。

モンテカルロ法で円周率を求める方法

\( x,\;y \) 座標において、中心が \( (0,\;0) \) の一辺が \( 2 \) の正方形と、中心が \( (0,\;0) \) で半径 \( 1 \) の円を考えます。

正方形の面積を \( S_{square} \) 、円の面積を \( S_{circle} \) とすると以下となります。

$$ S_{square} = 2 \times 2 = 4 $$

$$ S_{circle} = \pi \times 1 \times 1 = \pi $$

また、円と正方形の面積比 \( r \) は以下となります。

$$ r = \frac{\pi}{4} $$

次に、正方形内にランダムに1,000個の点を打点してみましょう。

以下、統計解析言語Rによりシミュレーションします。
input:

# 正方形内(-1,1)×(-1,1)の打点数
N <- 1000
x <- runif(N,-1,1)
y <- runif(N,-1,1)

# 正方形内(-1,1)×(-1,1)への打点と半径1の円の描画
curve( sqrt(1-x^2), xlim=c(-1,1), ylim=c(-1,1), asp=1, xlab="x", ylab="y")
curve(-sqrt(1-x^2), xlim=c(-1,1), ylim=c(-1,1), add=T)
points(x,y,xlim=c(-1,1),ylim=c(-1,1),add=TRUE)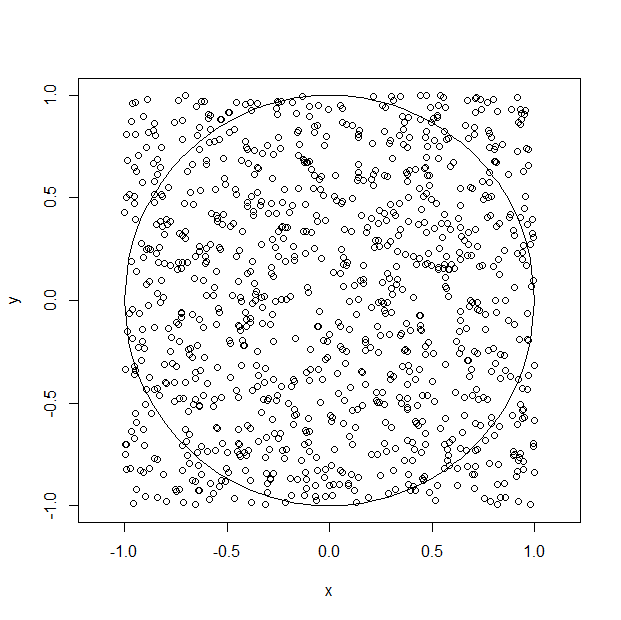

円内の打点数を \( n \)、正方形内の打点数を \( N \) とします。

ここで、正方形内にランダムに打点しているので、円内の打点数 \( n \) と正方形内の打点数 \( N \) の比は、円の面積と正方形の面積の比 \( r \) と等しくなります。

従って、 \( \pi \) は以下となります。

$$ \pi = 4 \times \frac{n}{N} $$

シミュレーション

正方形内の打点数 \( N \) を100、1,000、10,000、100,000の4パターンに分けてシミュレーションします。

さらに各パターンで100回試行し、標本数を100に増やしています。

標本数を増やすことで、よりランダムなシミュレーションができます。

以下、統計解析言語Rによるシミュレーションになります。
input:

# 総点数
hit_cnt_order <- 4
N <- numeric(hit_cnt_order)
for(i in 1:hit_cnt_order){
	N[i] <- 100*10^(i-1)
}

# 誤差配列の定義
n <- 100
# インナーループ誤差
error_inner <- numeric(n)
# アウターループ誤差
error_outer_mean <- numeric(hit_cnt_order)
error_outer_sd <- numeric(hit_cnt_order)

# πの推定値ベクトル
pi_estimate_vec <- numeric(n)

for(i in 1:hit_cnt_order){
	for(j in 1:n){
		# (-1,1)×(-1,1)にランダムに打点
		square <- cbind(runif(N[i],-1,1),runif(N[i],-1,1))

		# 中心(0,0)、半径1の円内の打点数
		circle <- sum(ifelse(square[,1]^2+square[,2]^2<=1,1,0))

		# πの推定
		pi_estimate_vec[j] <- 4*circle/N[i]

		# 真のπとの誤差
		error_inner[j] <- abs(pi - pi_estimate_vec[j])
	}
	# πの推定行列
	if(i==1){
		pi_estimate <- pi_estimate_vec
	}else{
		pi_estimate <- cbind(pi_estimate, pi_estimate_vec)	
	}
	# 誤差の平均
	error_outer_mean[i] <- mean(error_inner)
	# 誤差の標準偏差
	error_outer_sd[i] <- sqrt(var(error_inner)*(n-1)/n)
}

# 2×2分割プロット
par(mfrow=c(2,2)) 
hist(pi_estimate[,1],breaks = 20,xlab="pi estimation",main="N=100")
hist(pi_estimate[,2],breaks = 20,xlab="pi estimation",main="N=1000")
hist(pi_estimate[,3],breaks = 20,xlab="pi estimation",main="N=10000")
hist(pi_estimate[,4],breaks = 20,xlab="pi estimation",main="N=100000")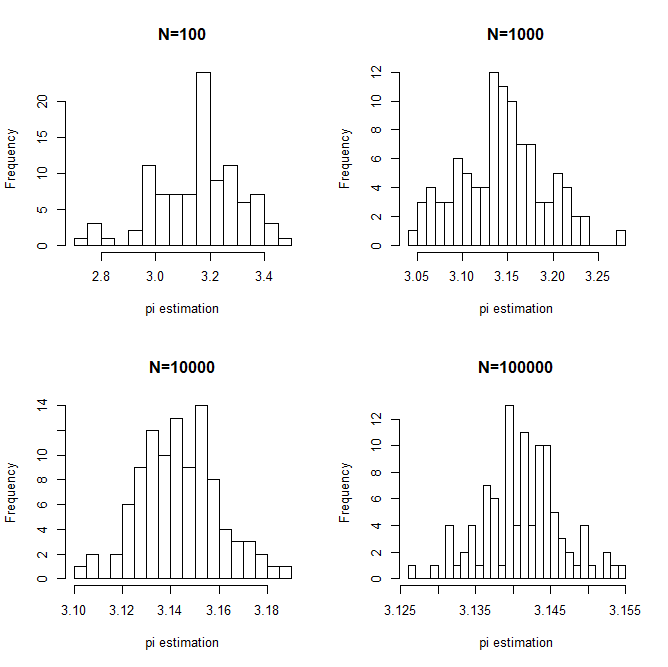

正方形内の打点数 \( N \) が100、1,000、10,000、100,000の場合に分けて、円周率 \( \pi \) のシミュレーション結果をヒストグラムで比較します。

\( N \) が増加するごとに、真の円周率 \( \pi \) に収束していく様子がわかります。

また、ヒストグラムの \( x \) 軸の幅が縮小していく様子も確認できます。

以下により、平均と標準偏差を計算します。
input:

# 平均、標準偏差の定義
mean_pi <- numeric(4)
sd_pi <- numeric(4)

for(i in 1:4){
	mean_pi[i] <- mean(pi_estimate[,i])
	sd_pi[i] <- sqrt(var(pi_estimate[,i])*(length(pi_estimate[,i]-1)/length(pi_estimate[,i])))
}

# 平均、標準偏差行列
cbind(mean_pi, sd_pi)

output:

      mean_pi       sd_pi
[1,] 3.161600 0.155691485
[2,] 3.144840 0.047411527
[3,] 3.143668 0.016545260
[4,] 3.141268 0.005341314

\( N \) が増加するごとに、平均値が真の円周率 \( \pi \) に収束し、誤差も縮小していくことが確認できました。