多変量適応的回帰スプライン(MARS)をPythonで試してみる

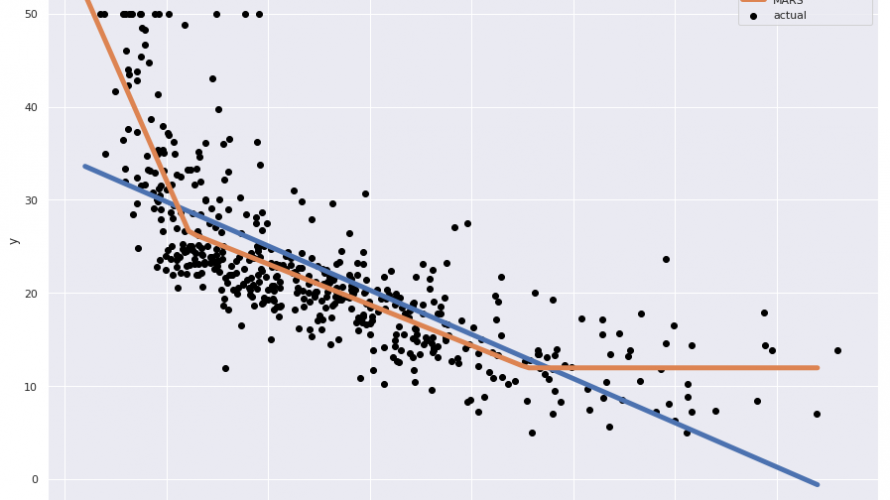
先日、MediumでMARS(Multivariate Adaptive Regression Splines:多変量適応的回帰スプライン)に関する記事を読みました。

Medium

 

1 User

133 Pockets

MARS: Multivariate Adaptive Regression Splines — How to Improve on Linear Reg...

https://towardsdatascience.com/mars-multivariate-adaptive-regression-splines-how-to-improve-on-linear-regression-e1e7a63c5eae

A visual explanation of the MARS algorithm with Python examples and comparison to linear regression

コードはGitHubに上がっています。

多変量適応的回帰スプライン(MARS)とは

多変量適応的回帰スプライン（Multivariate Adaptive Regression Splines, 以降は略してMARS）という厳つい名前ですが、文字通り線形回帰の一種です。
MARSと線形回帰との大きな違いは、MARSを使うことで非線形な観測値もモデリングできるという点です。
これはMARSが以下のようにヒンジ関数の線形結合によって目的変数を記述しているためです。
※ヒンジ関数は後述します。
$$
\hat{f(x)} = \sum_{i=1}^{k}c_i B_i(x)
$$

ここで \(c_i\) は定数で、 \(B_i(x)\) は以下のいずれかの関数となります。

• 定数
  切片を表現したい場合は \(B_i(x)\) は定数となります。
• ヒンジ関数
  後述しますが、 \(\max(0, x-c)\) または \(\max(0, c-x)\) で定義される関数です。
• 複数のヒンジ関数の掛け合わせ
  ヒンジ関数で交互作用項を表現したものです。
  例えば、 \(c_1 \cdot \max(0, x_1 – 1.1) + c_2 \cdot \max(0, x_1-0.9)\ \cdots\) など。

ヒンジ関数とは

ヒンジ関数(hinge function)は以下で定義されます。
$$
\max(0, x-c) \,\, \mbox{or} \,\, \max(0, c-x)
$$
ここで、 \(c\) は定数です。
定義だけだと分かりにくいので、ヒンジ関数を可視化してみましょう。
以下は \( \max(0, x-3) \) と、 \( \max(0, 3-x) \) をPythonで可視化した結果になります。
INPUT:

def hinge(x: np.array, c: int, mirror_f=False):
    """
    ヒンジ関数の一例
    """
    if mirror_f:
        return np.where(x-c>0, x-c, 0)
    else:
        return np.where(c-x>0, c-x, 0)


x = np.linspace(2.0, 4.0, 100)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, hinge(x=x, c=3), label='max(0, c-x)')
ax.plot(x, hinge(x=x, c=3, mirror_f=True), label='max(0, x-c)')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend()
ax.set_title('hinge function')
plt.show()

OUTPUT: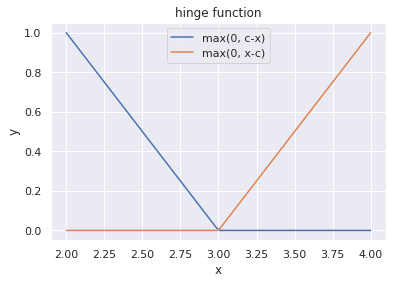

MARSでは、このようなヒンジ関数を線形結合することによって非線形な観測値に対するモデリングが可能になります。

Pythonで実践

以降ではPythonでMARSを実装したpy-earthライブラリを使って、MARSと線形回帰を比較してみます。
ちなみになぜ「earth」なのかというと、Wikipedia曰く、「MARS」という名前がすでに商標登録されているため、同名でのオープンソース実装を避けたいからとのこと。

使用するデータセットは、scikit-learnでおなじみのボストンの住宅価格データです。
いったん、MARSによるモデリングが効きそうな説明変数を選ぶために、各説明変数とターゲット変数の散布図をプロットします。
INPUT:

from sklearn.datasets import load_boston

# scikit-learnがデフォルトで持っているボストンの住宅価格データ
boston = load_boston()

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# 特徴量別にターゲット変数であるPriceとの関係性を確認する
fig = plt.figure(figsize=(20,20))
for num, col in enumerate(boston['feature_names']):
    ax = fig.add_subplot(4,4,num+1)
    ax.scatter(boston['data'][:, num], boston['target'])
    ax.set_title(col)

OUTPUT: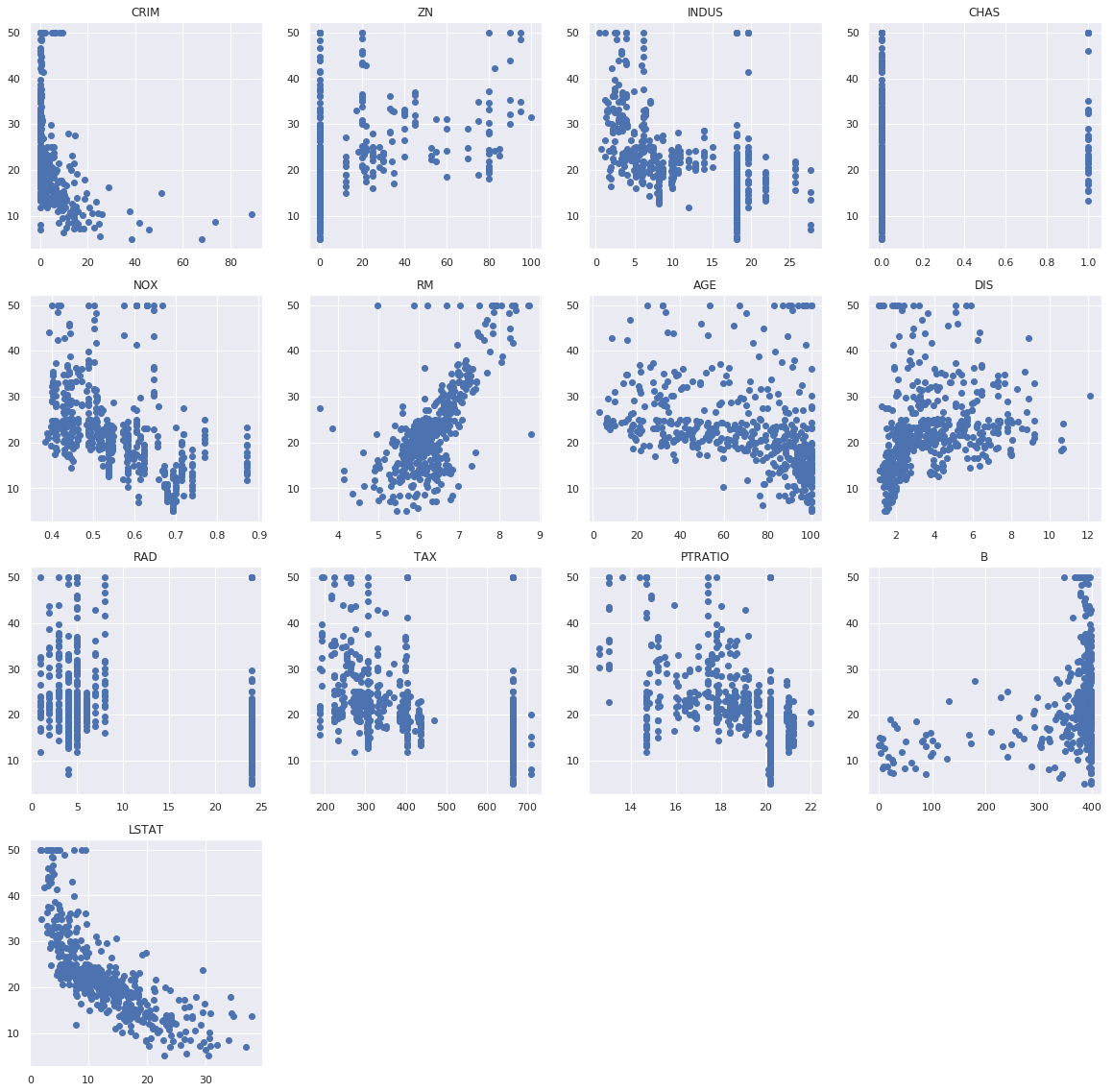

散布図を見るに、観測値に非線形性があって題材として適切な変数は「LSTAT」だと思うので、今回は説明変数をLSTAT、ターゲット変数をPRICEとして、MARSと線形回帰を比較することにします。
MARSと線形回帰それぞれでモデリングし、MARSのモデリング結果を確認します。
INPUT:

import pyearth
from sklearn.linear_model import LinearRegression

# ターゲット変数、説明変数を抽出
y = boston['target']
X = boston['data'][:, -1].reshape(-1,1)

LR = LinearRegression()
MARS = pyearth.Earth()

LR.fit(X, y)
MARS.fit(X, y)
# MARSモデルのサマリー
print(MARS.summary())

OUTPUT:

Earth Model
-------------------------------------
Basis Function  Pruned  Coefficient  
-------------------------------------
(Intercept)     No      11.9581      
h(x0-6.12)      Yes     None         
h(6.12-x0)      No      4.11806      
h(x0-22.74)     Yes     None         
h(22.74-x0)     No      0.87503      
x0              Yes     None         
-------------------------------------
MSE: 26.4084, GCV: 27.0460, RSQ: 0.6872, GRSQ: 0.6809

MARSモデルのサマリーより、観測値でモデリングすると以下の回帰式となることが分かります。
※GCV(一般化クロスバリデーション)等、出力されている指標に関しての説明は英語版Wikipediaに記載されています。

回帰式の \(\max(6.12 – x_0)\) 、 \(\max(22.74 – x_0)\) の2項から、傾きが変わる点が2つ存在することが分かります。
この2点はノット(knots)と呼ばれ、GCV(一般化クロスバリデーション)を使用した剪定によって最適なノット数が決まります。
※詳しくはこちらをご参照ください。
ここで、\(x_0\)は説明変数のLSTATを意味しています。
最後にMARSと線形回帰の当てはめ結果を可視化して比較します。

# モデル可視化用のx軸
X_ = np.linspace(int(X.reshape(-1).min()), int(X.reshape(-1).max()), 100).reshape(-1,1)

fig = plt.figure(figsize=(15, 10))
ax = fig.add_subplot(111)
ax.plot(X_, LR.predict(X_), label='LinearRegression', linewidth=5)
ax.plot(X_, MARS.predict(X_), label='MARS', linewidth=5)
ax.scatter(X.reshape(-1), y, label='actual', color='black')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend()
ax.set_title('MARS and LinearRegression')
plt.show()

OUTPUT: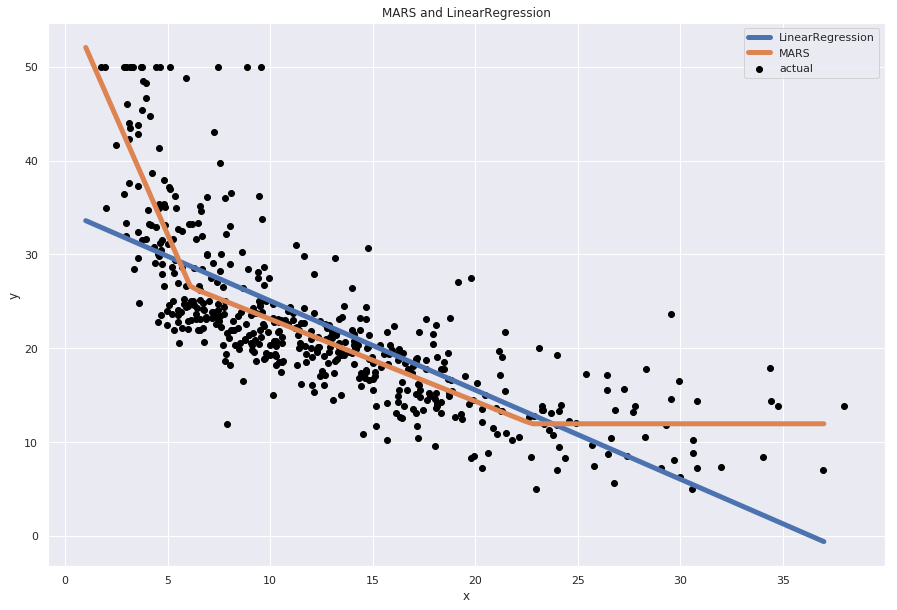

線形回帰(LinearRegression)では線形な関係性しか捉えられないですが、MARSでは非線形な関係性も捉えられています。
MARSがヒンジ関数の線形結合によって、非線形な観測値に対してもモデリングができることが分かります。

参考資料

• Multivariate adaptive regression spline(英語版Wikipedia)
• Multivariate Adaptive Regression Splines (MARS) in Python
• https://machinelearningmastery.com/multivariate-adaptive-regression-splines-mars-in-python/
• Chapter 7 Multivariate Adaptive Regression Splines