秘書問題をシミュレーションしてみた

無事に本社の忘年会が終わりました。

各部署の出し物のクオリティが全て高くて、「これ、忘年会の準備で業務に支障きたすレベルじゃね?（^^;）」って思ったり思わなかったり笑

さて、最近は『アルゴリズム思考術:問題解決の最強ツール』という本を読んでいます。

そこで、秘書問題という古典的な最適停止問題が取り上げられており、それがなかなか面白い内容だったので、今回は簡単なシミュレーションを交えて紹介します。
（本書のレビューは読了後にします。）

ちなみにサムネイル画像は『ゆかちぃ』こと河村友歌さんです。
ぱくたそというフリー素材サービスで名を馳せているとても可愛らしい女の子でーす。

ぱくたそ-フリー素材・無料写真ダウンロード

 

34 Posts

27 Shares

26 Users

19 Pockets

河村友歌 | ぱくたそ-フリー素材・無料写真ダウンロード

https://www.pakutaso.com/kawamurayuka.html

「河村友歌」の写真素材｜使って楽しい、見て楽しい。会員登録不要のフリー写真素材ぱくたそ

最適停止問題とは

ざっくりと言うと、どこまで見て、選び始めるのか、その基準を定める問題です。

例えば、物件探しは最適停止問題の１つです。

物件を探すときは、たいてい何軒か内見した上で、どの物件にするかを選びますね。

物件探しって、「他にもっといい物件があるのでは？」とか、「もたもたしていると他の人に物件を取られてしまう！」とか考えてしまって、なかなかどの段階で物件を選ぶべきか判断が難しいものです。

こういった、どこまで見て選び始めるべきなのかが難しい問題に関して、最適な閾値を求める問題が最適停止問題になります。

秘書問題とは

秘書の求人に応募してきた人を面接する立場になったと想定します。
以下のルールのもとで、最も優秀な秘書を採用するには、どのタイミングで選ぶべきでしょうか？

• 面接官は１人ずつランダムな順番で面接する
• 面接官はいつでも好きな人を採用しても良い
• 選んだ応募書は辞退できず、１人選んだ時点で選考は終了する
• 一度不採用とした応募者をあとから採用することはできない

実は、この問題に関しては数学的に37パーセントルールという最適解が与えられています。

100人の応募者から選ぶ場合は37人まで見て（このとき応募書は見るだけで選ばない）、38人目以降から良い応募者（見てきた37人より良い応募者）がいれば採用するということです。

秘書問題のシミュレーション

シミュレーションで秘書問題に37パーセントルールが最適解となっているかどうかを確かめてみます。

統計解析言語Rを使ってシミュレーションします。

100人の応募者に対して、何人目まで応募者を見て、選び始めるべきなのかを10,000回試行した確率でみてみます。

# 試行回数
try_cnt <- 10000
# 人数
n <- 100
# 秘書
secretary <- numeric(n)
# 確率分布
prob <- numeric(n)

# jは見る人数
for(j in 1:(n-1)){
  success <- 0
  for(i in 1:try_cnt){
    # ランダムに優先度割付
    secretary <- sample(1:n,n)
    # 基準値
    criterion_max <- 0
    # 成功数カウント
    excel_cnt <- 0
    for(k in 1:j){
      if(criterion_max < secretary[k]){
        criterion_max <- secretary[k]
      }
    }
    for(l in (j+1):n){
      if(criterion_max < secretary[l]){
        excel_cnt <- excel_cnt + 1
        criterion_max <- secretary[l]
      }
    }
    if(excel_cnt == 1){
      success <- success + 1
    }
  }
  prob[j] <- success / try_cnt
}
# 確率分布に行番号付与
rownum <- 1:n
distribution <- cbind(rownum,prob)
# グラフにプロット
plot(distribution,type="h")

出力結果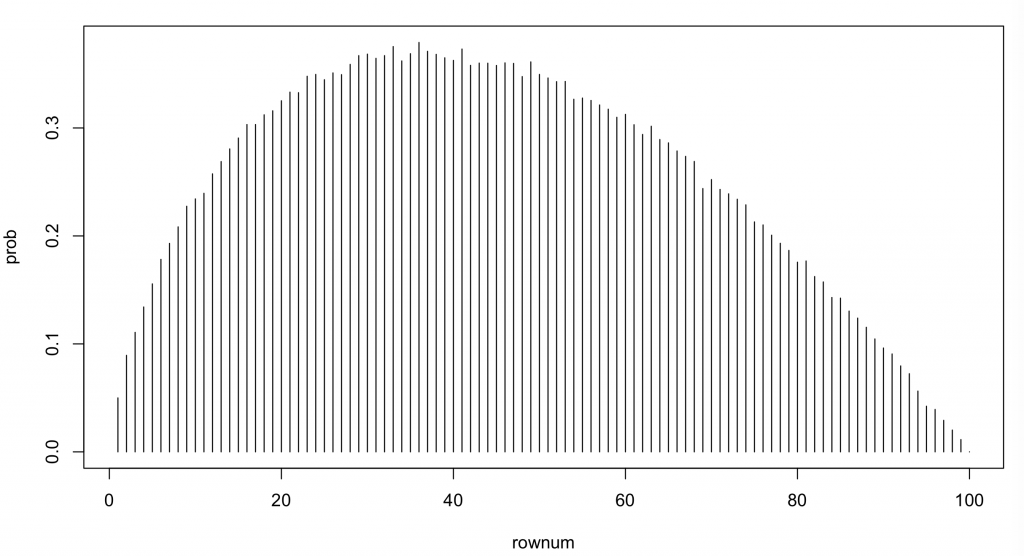

横軸は「何人目まで見るか」で、縦軸は「優秀な秘書を採用できる確率」になります。

30パーセント後半から40パーセント前半の確率が高いことがわかりますね。

詳細をみてます。

> distribution[distribution[,2]==max(distribution[,2]),]
 rownum    prob 
36.0000  0.3792

優秀な秘書を選ぶには36人目までを見てからが最適ということがわかりました。

37パーセントに限りなく近いですね。

数学的には \( n \) （応募者の人数）が限りなく大きいとき、37パーセントに収束することがわかっています。

秘書問題の数学的な証明

シミュレーション結果が数学的な最適解に沿っているのかどうか確かめます。

\( n \) 人の応募者の中から最も優秀な秘書を選びます。

\( k \; ( \; k \geq 1 \; ) \) 人までを選ばずに見るだけとして、\( t \; ( \; n \geq t \geq k+1 \;) \) 人目で最も優秀な秘書を選ぶ確率を考えます。

まず、\( t \) 人目に最も優秀な応募者がいる確率ですが、これは、異なる \( n \) 個の中から1つだけを選ぶ確率と同じなので、 \( 1 \; / \; n \) となります。

次に \( k+1 \) 人目から \( t-1 \) 人目までに、\( k \) 人目までに見たどの応募者よりも優秀な応募者がいない確率を求めます。

これは、 \( t-1 \) 人目までにおける最も優秀な応募者が \( k \) 人目までにいる確率であるので、\( k \; /\;(\; t-1 \; ) \) となります。

以上より、\( k \) 人目までを選ばずに見た場合に最も優秀な秘書を選べる確率 \( P\;(\; k \; ) \) は以下になります。
\begin{eqnarray}
P\;(\;k\;)\; &=& \frac{1}{n} \sum_{t=k+1}^{n}\frac{k}{t-1} \\
&=& \frac{k}{n}\left( \frac{1}{k} + \cdots + \frac{1}{n-1} \right)
\end{eqnarray}
ここで、右辺の分数和について、以下の近似式を用いて書き換えます。
$$ 1 + \frac{1}{2} + \cdots + \frac{1}{n} = \int_{1}^{n}\frac{1}{x}dx $$
すると、確率 \( P\;(\; k \; ) \) は以下になります。
\begin{eqnarray}
P\;(\;k\;)\; &=& \frac{k}{n} \int_{k}^{n}\frac{1}{x}dx \\
&=& \frac{k}{n} \;(\;\log \;(\; n \;)\; - \log \;(\; k\; )\;) \\
&=& \frac{k}{n}\log\frac{n}{k}
\end{eqnarray}
この \( P\;(\; k \; ) \) が最大となるような \( k \) を求めます。

\( P\;(\; k \; ) \) を \( k \) で微分します。
$$ \frac{d}{dx} P\;(\;k\;)\; = \frac{1}{n}\log \frac{n}{k} - \frac{1}{n} $$
したがって \( \; P\;'(\; k \; )=0 \) が成立するのは \( k = n \; / \;e \) を満たすときであり、このとき \( P\;(\; k \; ) \)　は最大値をとります。

最後に、この \( k \) が応募者全員 \( n \) のうち、どの割合に位置しているのかを計算します。
\begin{eqnarray}
\frac{n}{e} \times \frac{1}{n} &=& \frac{1}{e} \\
&=& 0.3678794\cdots
\end{eqnarray}
ほぼ37パーセントですね。

よって、全体の37パーセントの人数までを選ばずに見て、それ以降で応募者を選ぶべきだということが数学的にも証明されました。