PythonでROC曲線における最適なカットオフ値を算出する方法

2020.08.02
統計解析
ROC

ROC曲線って、使わないとすぐに解釈の仕方を忘れてしまいます。
縦軸や横軸が何を表していて、何を基準にプロットしていくのか、毎回使うときにググってしまう今日この頃です。

ということで、今回は自分の記憶の整理をかねてROC曲線の可視化を実施し、最適なカットオフ値を算出するYouden index(Youden’s J statistic)を用いた方法も紹介します。
さらに、scikit-learnライブラリでロードできるウィスコンシン州における肺がんのデータセットを使用して、実際にYouden indexを用いてカットオフ値を算出し、モデルの精度が向上することを確認します。

1. ROC曲線とは
2. Youden indexを用いたカットオフ値の算出方法
3. 肺がんデータセットで試してみる
4. 最後に
5. 参考

ROC曲線とは

ROC曲線は分類タスクにおいてモデルを評価する際に使われるグラフです。任意に設定したカットオフ値における真陽性率と偽陽性率をプロットします。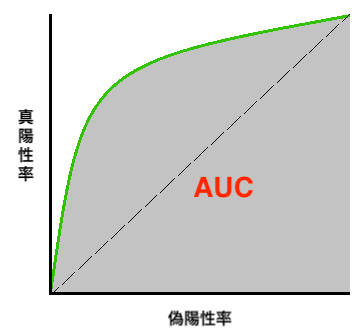

ここで、真陽性率、偽陽性率を簡単に説明すると以下になります。

真陽性率：陽性のデータのうち、モデルが陽性と判断できたデータの割合
偽陽性率：陰性のデータのうち、モデルが陽性と判断したなかで陰性だったデータの割合

ROC曲線でモデルを評価する際に一般的なのはAUC(Area Under Curve)です。
AUCはROC曲線の下側の面積のことで、AUCが高いほどモデルの分類性能が高いといえます。
ただし、AUCはあくまでモデルの全体的な分類性能を評価を示すだけで、具体的にどのカットオフ値を選べば良いのかを定量的に判断することはできません。
この問題を解決するのが次に説明するYouden indexを使った方法です。

ROC曲線に関してはこちらでかなり詳しく説明されています。

Youden indexを用いたカットオフ値の算出方法

ROC曲線をもとに最適なカットオフ値を定量的に算出するためには、Youden index(YoudenのJ統計量)を用います。
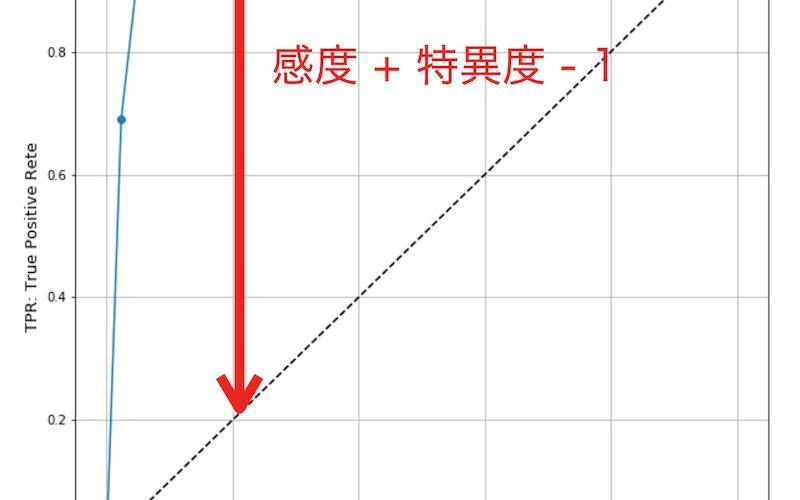
これは、分類精度が最も低いROC曲線となる直線(AUCが0.5)から最も離れた点をカットオフ値にする方法です。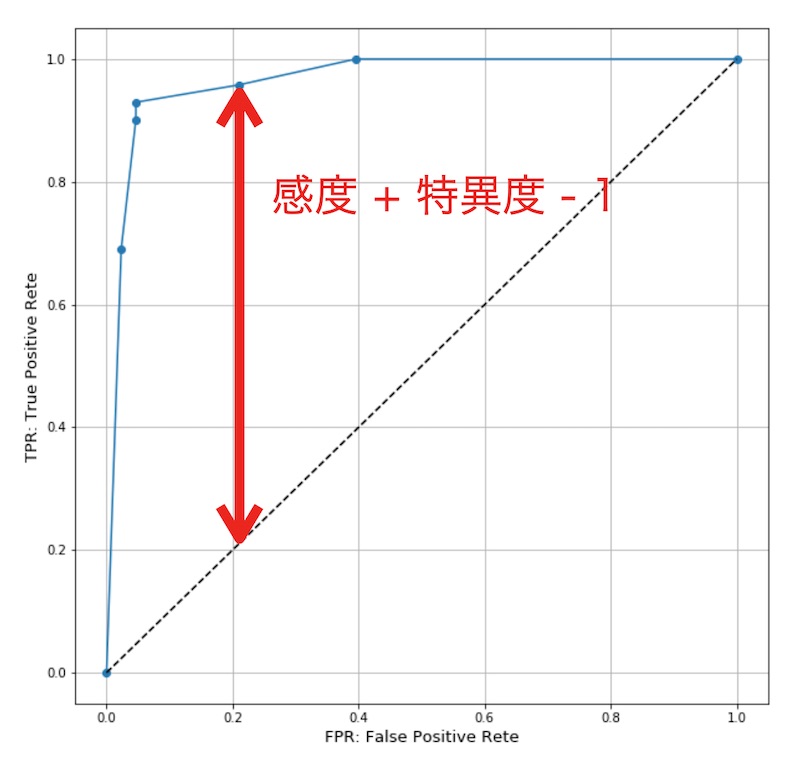

上図で示した通り、「感度+特異度-1」が最大となる点が最適なカットオフ値です。
ここで、感度と特異度は病気を診断する際の尺度として用いられる用語で、以下で定義されます。

感度：真陽性率(TRP)
特異度：1-偽陽性率(1-FRP)

すなわち、ROC曲線の全てのカットオフ値において「真陽性率(TRP)-偽陽性率(FRP)」を算出し、最大値をとるカットオフ値が最適値となります。

肺がんデータセットで試してみる

実データでYouden indexを用いたカットオフ値を算出し、デフォルトのカットオフ値(0.5)の場合よりもモデルの分類精度が向上することを確かめます。
実データとして、scikit-learnライブラリからロードできるウィスコンシン州における肺がんのデータセットを使用します。

まず、複数の分類モデルでROC曲線を描画し、モデルの分類精度を比較します。
比較するモデルはロジスティック回帰、決定木、K近傍、ガウシアンナイーブベイズです。
なお、今回は最適なカットオフ値による分類精度の向上を確認したいだけなので、モデルではデフォルトのパラメータとしています。
また、ある程度分類精度を低下させるため、ランダムに使用するカラムを抽出したり、学習データセット数を削減したりしています。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix, roc_curve

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
# 乱数シードを固定
random.seed(0)

# 肺ガンデータセットをロード
data = load_breast_cancer()

# あえてカラムを絞ってモデルの分類精度を下げる
selected_feature_index = np.array(random.sample(range(len(data.feature_names)), k=3)) + 1
print(f'target columns: {data.feature_names[selected_feature_index]}')

# 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
    data.data[:, selected_feature_index],
    data.target,train_size=0.8, test_size=0.2, random_state=42)

# 分類モデル初期化
models = [
    LogisticRegression(),
    DecisionTreeClassifier(),
    KNeighborsClassifier(),
    GaussianNB()
]

# 学習
models = [model.fit(X_train, y_train) for model in models]

cutoff_criterions = list()

fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111)
for model in models:
    model_name = model.__class__.__name__
    fpr, tpr, thres = roc_curve(y_test, model.predict_proba(X_test)[:, 1])
    auc = metrics.auc(fpr, tpr)
    # 特異度
    sng = 1 - fpr
    # Youden indexを用いたカットオフ基準
    cutoff_criterion = tpr + sng - 1
    cutoff_criterions.append(cutoff_criterion)
    print(f'{model_name}, auc:{auc}')
    ax.plot(fpr, tpr, marker='o', label=model_name)    
ax.legend()
ax.grid()
ax.set_xlabel('FPR: False Positive Rete', fontsize = 13)
ax.set_ylabel('TPR: True Positive Rete', fontsize = 13)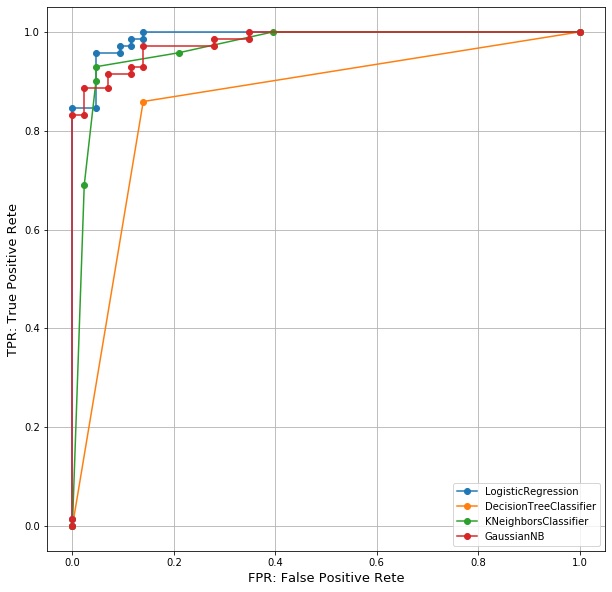

ロジスティック回帰モデルのAUCが最も高いため、ロジスティック回帰モデルの分類精度が最も良いと言えそうです。
ただ、AUCでわかるのはモデルの全体的な分類精度だけで、具体的にどのカットオフ値を選択すれば良いのかはわかりません。
ここで、ロジスティック回帰モデルについて、Youden indexを用いて算出したカットオフ値とデフォルトのカットオフ値（0.5）の場合の分類結果を比較してみます。

# Youden indexによるカットオフ値による分類
y_pred_cutoff = models[0].predict_proba(X_test)[:, 1] >= cutoff_criterions[0]
# 混同行列をヒートマップで可視化
fig = plt.figure(figsize=(20,7))
ax = fig.add_subplot(121)
cm = confusion_matrix(y_test, y_pred_cutoff)
sns.heatmap(cm, annot=True, cmap='Blues', ax=ax)
ax.set_title('cutoff (Youden index)')

ax = fig.add_subplot(122)
cm = confusion_matrix(y_test, model.predict(X_test))
sns.heatmap(cm, annot=True, cmap='Blues', ax=ax)
ax.set_title('cutoff (Default)')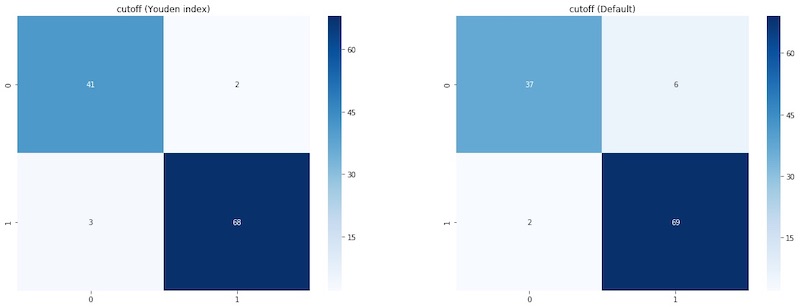

左はYouden indexを用いたカットオフ値の混同行列で、右はデフォルトのカットオフ値（0.5）の混同行列です。
明らかにYouden indexを用いたカットオフ値の方がモデルの分類精度が上がっていることがわかりました。