決定木アルゴリズムの重要度(importance)を正しく解釈しよう

機械学習案件で、どの特徴量がターゲットの分類で「重要」かを知るためにRandamForestやXGBoostなどの決定木系アルゴリズムの重要度(importance)を確認するということがよくあります。
ただ、この重要度がどのように計算されているのかを知らずに、なんとなく「重要」な特徴量をあぶり出してくれる便利なツールとして使われていまっているような印象があります。
確かに重要度はお手頃に求められる指標でいかにも特徴量の「重要」度を良く説明しているように見えますが、実際にどれくらいターゲットの分類で効いているのかを聞かれると答えに窮してしまいます。
(どの特徴量がどの程度の値になれば、精度がどの程度改善するのか?などの定量的な質問)
今回は決定木アルゴリズムにおける重要度とは何かを正しく理解して、正しく解釈できるようになることを目指します。
※2021/2/12追記:「特徴量重要度だけではなく部分依存グラフを使ってみよう」という記事を書きました。
今回ご紹介する重要度の計算は、scikit-learnで実装されている方法に基づいています。
また、回帰ではなく、分類の場合の重要度の計算を説明しています
重要度(Importance)とは何か
乱暴な言い方をすると、重要度(importance)とは「その特徴量の分割がターゲットの分類にどれくらい寄与しているかを測る指標」です。
重要度は、以下で説明するジニ不純度(Gini impurity)をもとに計算できます。
ジニ不純度(Gini impurity)
ノードごとに「ターゲットがどれくらい分類できていないか」を測る指標です。
あるノードにおけるジニ不純度(Gini impurity)は以下で定義されます。
$$ G(k) = \sum_{i=1}^{n} p(i) \times (1-p(i)) $$
- \( G(k) \) : あるノード \( k \) における不純度
- \( n \) : ターゲットラベルの数
- \( p(i) \) : あるノード \( k \) におけるターゲットラベル \( i \) の頻度
上記の定義から、ノードにおいて完全にサンプルが分類されている場合はジニ不純度は0になります。
重要度(importance)
上で説明したジニ不純度(Gini impurity)をもとに重要度(importance)が計算されます。
もう少し掘り下げると、重要度は「ある特徴量で分割することでどれくらいジニ不純度を下げられるのか」を意味しています。
ある特徴量 \( j \) における重要度は以下で定義されます。
- \( I(j) \) : ある特徴量 \( j \) における重要度
- \( F(j) \) : ある特徴量 \( j \) が分割対象となるノードの集合
- \( N_{parent}\,\,(i) \) : あるノード \( i \) におけるサンプル数
- \( N_{left\_child}\,\,(i) \) : あるノード \( i \) の子ノードのうち左側のノードのサンプル数
- \( N_{right\_child}\,\,(i) \) : あるノード \( i \) の子ノードのうち右側のノードのサンプル数
- \( G_{parent}\,\,(i) \) : あるノード \( i \) におけるジニ不純度
- \( G_{left\_child}\,\,(i) \) : あるノード \( i \) の子ノードのうち左側のノードにおけるジニ不純度
- \( G_{right\_child}\,\,(i) \) : あるノード \( i \) の子ノードのうち右側のノードにおけるジニ不純度
定義のみだとわかりにくいので、具体例を挙げて説明します。
example
irisデータセットを使って決定木をみてみましょう。
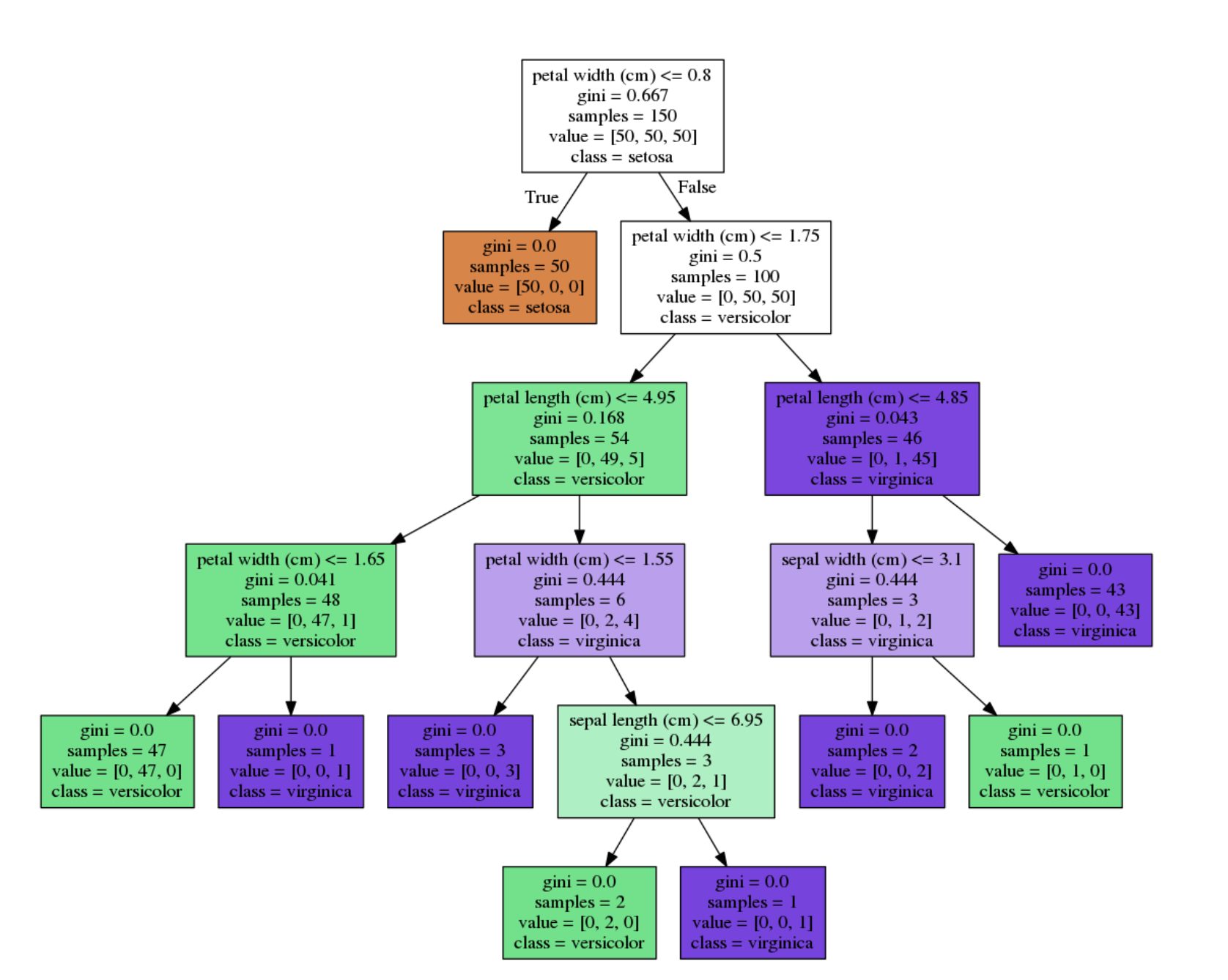
ジニ不純度
1番上(ルートノード: \( r \) )のジニ不純度を計算します。
G(r) & = & \sum_{i=1}^{3} p(i) \times (1-p(i)) \\
& = & \frac{50}{150} \times \left( 1-\frac{50}{150} \right) + \frac{50}{150} \times \left( 1-\frac{50}{150} \right) + \frac{50}{150} \times \left( 1-\frac{50}{150} \right) \\
& = & 0.667
\end{eqnarray}
重要度
特徴量の一つであるsepal widthの重要度を計算します。
sepal widthは深さ4のノードで分割されていて、1つのノードでしか分割されていません。
\begin{eqnarray}
I(sepal\ width) & = & (3 \times 0.444) – (2 \times 0.0 + 1 \times 0.0) \\
& = & 1.332
\end{eqnarray}
特徴量や木の深さと重要度(Importance)との関係性を考察
KaggleのTitanicデータセットを使ってシンプルな決定木を作って、特徴量や木の深さがどう重要度(Importance)に影響を及ぼしていくのかを考察していきます。
準備
以下のコマンドにより決定木の可視化に必要なライブラリをインストールします。
brew install graphviz
pip install graphviz
pip install dtreevizデータを読み込み、決定木に入力させるために特徴量を加工します。
今回は説明のしやすさを重視しモデルを簡略化させるために、Pclass、Sex、Fareのみに特徴量を絞ります。
データ読み込み加工
import pandas as pd
from dtreeviz.trees import dtreeviz
import graphviz
from sklearn.tree import export_graphviz
from sklearn import tree
from sklearn.preprocessing import LabelEncoder
# データ読み込み
train = pd.read_csv('../data/train.csv')
# ターゲット変数
target = ['Survived']
# 今回使用する特徴量
features = ['Pclass', 'Sex', 'Fare']
# カテゴリカル変数
cat_cols = ['Pclass', 'Sex']
# ラベル辞書作成
# ラベルエンコーディング
label_dict = {}
for col in cat_cols:
le = LabelEncoder()
train.loc[:, col] = le.fit_transform(train[col])
label_dict[col] = le.classes_決定木(decision tree)の構築(depth:2)
まずは深さ2の決定木を構築し、重要度をみてみましょう。
# 深さ2の決定木を構築
clf = tree.DecisionTreeClassifier(max_depth=2)
clf.fit(train[features], train[target])
# 木を可視化
export_graphviz(
clf,
out_file='tree.dot',
class_names=['death', 'survived'],
feature_names=features,
filled=True
)
with open('tree.dot') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)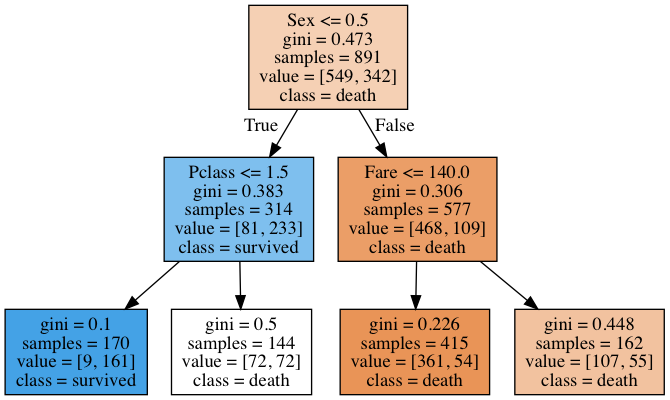
上記の出力された結果をもとに特徴量の重要度それぞれを算出します。
(ジニ不純度についての計算は省きます。出力されたグラフに記載されたジニ不純度をもとに重要度を計算します。)
\begin{eqnarray}
I(Pclass) & = & (314 \times 0.383) – (170 \times 0.1 + 144 \times 0.5) \\
& = & 31.262
\end{eqnarray}
\begin{eqnarray}
I(Sex) & = & (891 \times 0.473) – (314 \times 0.383 + 577 \times 0.306) \\
& = & 124.619
\end{eqnarray}
\begin{eqnarray}
I(Fare) & = & (577 \times 0.306) – (415 \times 0.226 + 162 \times 0.448) \\
& = & 10.196
\end{eqnarray}
ここで、scikit-learnで出力される重要度は正規化されているので、同様に重要度の合計でそれぞれの特徴量を割り、重要度を計算し直します。
- \( I(Pclass) = 31.262/166.077 = 0.188237986 \)
- \( I(Sex) = 124.619/166.077 = 0.750368805 \)
- \( I(Fare) = 10.196/166.077 = 0.061393209 \)
では、scikit-learnで出力される重要度と比較してみましょう。
for n, v in zip(features, clf.feature_importances_):
print(f'importance of {n} is :{v}')importance of Pclass is :0.18794916264968867 importance of Sex is :0.7504324135604815 importance of Fare is :0.06161842378982976
ほぼ同じ値が出力されていることを確認できました。
決定木(decision tree)の構築(depth:3)
# 深さ4の決定木を構築
clf = tree.DecisionTreeClassifier(max_depth=4)
clf.fit(train[features], train[target])
# 木を可視化
export_graphviz(
clf,
out_file='tree.dot',
class_names=['death', 'survived'],
feature_names=features,
filled=True
)
with open('tree.dot') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)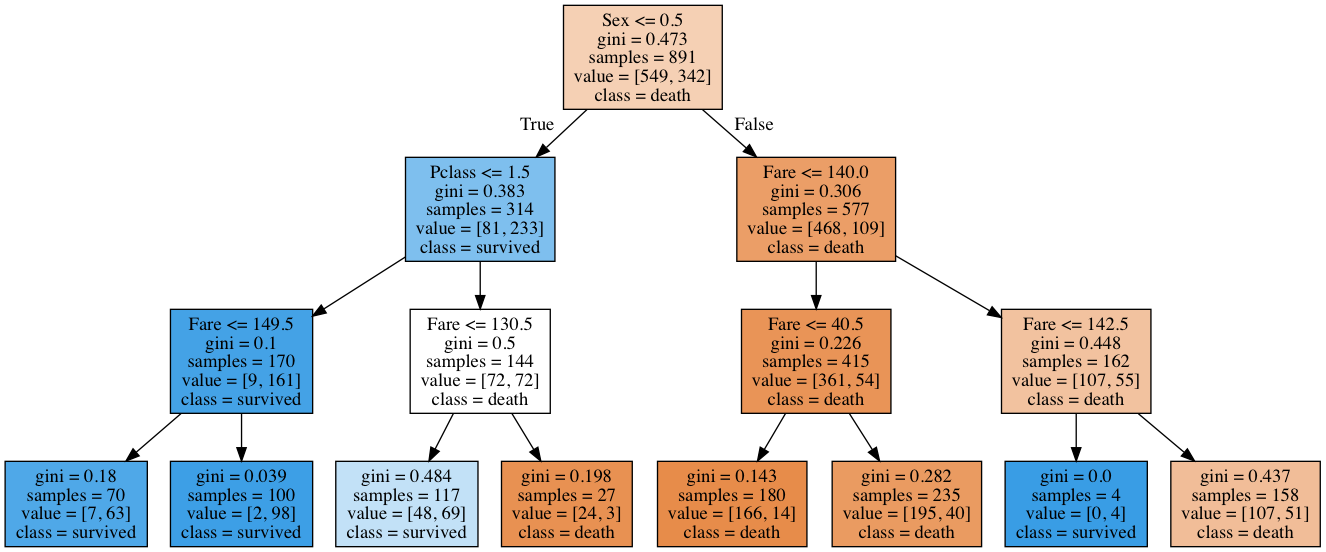
\begin{eqnarray}
I(Pclass) & = & (314 \times 0.383) – (170 \times 0.1 + 144 \times 0.5) \\
& = & 31.262
\end{eqnarray}
\begin{eqnarray}
I(Sex) & = & (891 \times 0.473) – (314 \times 0.383 + 577 \times 0.306) \\
& = & 124.619
\end{eqnarray}
Fareに関しては分割対象になっているノード数が多いので、分割対象の親ノードごとの重要度を計算後に合算します。
$$ I(Fare_1) = (577 \times 0.306) – (415 \times 0.226 + 162 \times 0.448) = 10.196 $$
$$
I(Fare_2) = (170 \times 0.1) – (70 \times 0.18 + 100 \times 0.039) = 0.5
$$
$$
I(Fare_3) = (144 \times 0.5) – (117 \times 0.484 + 27 \times 0.198) = 10.026
$$
$$
I(Fare_4) = (415 \times 0.226) – (180 \times 0.143 + 235 \times 0.282) = 1.78
$$
$$
I(Fare_5) = (162 \times 0.448) – (4 \times 0.0 + 158 \times 0.437 = 3.53
$$
よって
$$
I(Fare) = 10.196 + 0.5 + 10.026 + 1.78 + 3.53 = 26.032
$$
重要度をを正規化すると以下になります。
- \( I(Pclass) = 31.262/181.913 = 0.17185138 \)
- \( I(Sex) = 124.619/181.913 = 0.685047248 \)
- \( I(Fare) = 26.032/181.913 = 0.143101373 \)
scikit-learnの出力結果と比較してみます。
for n, v in zip(features, clf.feature_importances_):
print(f'importance of {n} is :{v}')importance of Pclass is :0.17150429334382816 importance of Sex is :0.6847723021244702 importance of Fare is :0.1437234045317016
ほぼ同じ値が出力されていることを確認できました。
考察
決定木が深くなるに連れて数値特徴量であるFareが分割対象となるノードの数が増えていっています。
重要度(Importance)の定義では、分割対象のノード数が増えるほどその特徴量の重要度は相対的に増加していきます。
カテゴリカル変数の場合は分割分岐点の数がカテゴリ数に依存しますが、数値特徴量は分割分岐点をどこにでも取ることができます。
したがって、数値特徴量の場合、木が深くなるごとに重要度が相対的に高く出てしまう可能性が高くなると言えそうです。
まとめ
決定木アルゴリズムの重要度(importance)は、木が深くなるほどに特徴量のカテゴリ数や数値型の特徴量による影響を大きく受けることがわかりました。
決定木アルゴリズム(特によく使われるRandamForestやXGBoost)は特徴量のスケールや離散化をせずに使用できる点でかなり便利な代物ですが、はじき出される重要度を鵜呑みにするのは危険です。
そもそも、重要度は「ターゲットの分類にその特徴量による分割がどれくらい寄与しているかを測る指標」なのであって、具体的にどの特徴量をどれくらいの値にすると結果がどうなるのかは言えません。
古典的な重回帰モデルがいまだに好まれる理由はここにあります。
ある変数をどれくらいの値にすることでどれだけターゲットの値が変化するのかがわかるのが重回帰モデルの良いところです。
特徴量をゴリゴリ加工しなければならないのが欠点ではありますが、今一度見直してみるのも悪くないと思います。
参考資料
- 前の記事

Appleが公開している機械学習ライブラリTuri CreateでKaggle Titanicをやってみる 2019.09.10
- 次の記事
施策効果の測定にはベイジアンA/Bテストを使おう! 2019.10.13