住宅価格を予測する〜Kaggle House Priceチュートリアルに挑む

日増しに寒くなってきました。
街ゆく人々は厚手のコートにマフラーと本気で防寒し始めているわけですが、著者はダイエットのためにあえて薄着で過ごしております。

さて、Kaggleの回帰問題のチュートリアルである、住宅価格の予測(House Prices: Advanced Regression Techniques)に挑戦しました。

Kaggleには2つチュートリアルがあって、回帰問題はHouse Price、クラス分類問題はタイタニック号の乗客の生存予測(Titanic: Machine Learning from Disaster)になります。

www.kaggle.com

 

251 Shares

9 Users

248 Pockets

House Prices: Advanced Regression Techniques

https://www.kaggle.com/c/house-prices-advanced-regression-techniques

Predict sales prices and practice feature engineering, RFs, and gradient boosting

キヨシの命題

 

2 Pockets

タイタニック号の乗客の生存予測～Kaggleに挑戦（その１）

https://yolo-kiyoshi.com/2017/11/15/post-499

だんだん冬が近づいてきましたね。そろそろシャツ1枚で外出するのは、世間体的に宜しくないシーズンとなってまいりました。さて、今回はKaggleという統計学を学んだ者にとっては胸が熱くなるようなサービスがあったので、統計解析手法の復習もかねてチャレンジしてみようと思います！（まずはKaggleにアプライすることをゴールにしています、、、）お題はタイタニック号の乗客の生存予測です。タイタニック号の沈没事故は皆さん映画で良くご存知だと思いますので、説明は省略します。当時の乗客のデータを使って、どんな乗客なら生存し...

このチュートリアルの目的はいたって簡単で、与えられた79もの変数(敷地面積とか天井の高さとか)をもとに住宅価格を予測するだけです。

今回は程々にデータを前処理し、なんとなく線形回帰モデルを構築してKaggleに予測結果を提出するまでを説明します。
ちなみにスコアは0.13110(4,748人中1,807位)で初めて挑んだにしてはなかなか良い成績でした^^

※2019/10/18情報追記：Exploratoryを使った方法を以下で紹介しています。

キヨシの命題

 

2 Pockets

ExploratoryでKaggleのHouse Priceをやってみる

https://yolo-kiyoshi.com/2019/10/18/post-1265

前回の投稿でベイジアンA/Bテストを紹介しましたが、その際に参考にした記事でExploratoryというツールが用いられていました。調べてみると、ExploratoryではベイジアンA/Bテストはもちろんのこと、データの可視化やモデル構築までできるとのこと。Public版なら無料で使えるので、今回はKaggleのHouse Priceチュートリアルを題材に、Exploratoryでどういうことができるのかを試してみます。ちなみに、KaggleのHouse Priceチュートリアルについては以下の記事で取り上げています。ExploratoryとはExploratoryを一言でいうと、データ分析...

以下、Pythonのver3.7で実行しています。

ライブラリの準備

今回使用するライブラリをインポートします。
input:

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import (
    LinearRegression,
    Ridge,
    Lasso
)
%matplotlib inline

前処理

データの取り込み

KaggleのHouse Priceのページからデータをダウンロードし、読み込みます。
学習データとテストデータをまとめて前処理するために、フラグをつけた上でマージしています。
input:

# データの読み込み
train = pd.read_csv('../input/train.csv') #訓練データ
test = pd.read_csv('../input/test.csv') #テストデータ
# 学習データとテストデータのマージ
train['WhatIsData'] = 'Train'
test['WhatIsData'] = 'Test'
test['SalePrice'] = 9999999999
alldata = pd.concat([train,test],axis=0).reset_index(drop=True)
print('The size of train is : ' + str(train.shape))
print('The size of test is : ' + str(test.shape))

output:

The size of train is : (1460, 82)
The size of test is : (1459, 82)

説明変数として関係がない、Id、SalePrice、WhatIsDataを除いて79もの変数があります。
扱う変数がかなり多く、一つずつ確認するのはかなり時間的にも精神的にも厳しいものです。
なので、以降では詳細な変数の説明はせず、最低限予測モデル構築に必要な処理をするにとどめます。

欠損値の補完

まず学習データとテストデータの欠損の有無を調べます。
input:

# 学習データの欠損状況
train.isnull().sum()[train.isnull().sum()>0].sort_values(ascending=False)

output:

PoolQC          1453
MiscFeature     1406
Alley           1369
Fence           1179
FireplaceQu      690
LotFrontage      259
GarageYrBlt       81
GarageType        81
GarageFinish      81
GarageQual        81
GarageCond        81
BsmtFinType2      38
BsmtExposure      38
BsmtFinType1      37
BsmtCond          37
BsmtQual          37
MasVnrArea         8
MasVnrType         8
Electrical         1
dtype: int64

input:

# テストデータの欠損状況
test.isnull().sum()[test.isnull().sum()>0].sort_values(ascending=False)

output:

PoolQC          1456
MiscFeature     1408
Alley           1352
Fence           1169
FireplaceQu      730
LotFrontage      227
GarageYrBlt       78
GarageCond        78
GarageQual        78
GarageFinish      78
GarageType        76
BsmtCond          45
BsmtExposure      44
BsmtQual          44
BsmtFinType1      42
BsmtFinType2      42
MasVnrType        16
MasVnrArea        15
MSZoning           4
BsmtFullBath       2
BsmtHalfBath       2
Utilities          2
Functional         2
Exterior2nd        1
Exterior1st        1
SaleType           1
BsmtFinSF1         1
BsmtFinSF2         1
BsmtUnfSF          1
KitchenQual        1
GarageCars         1
GarageArea         1
TotalBsmtSF        1
dtype: int64

また、欠損している変数が数値型なのかカテゴリカル変数なのかを把握するために、データ型も確認しておきます。
input:

# 欠損を含むカラムのデータ型を確認
na_col_list = alldata.isnull().sum()[alldata.isnull().sum()>0].index.tolist() # 欠損を含むカラムをリスト化
alldata[na_col_list].dtypes.sort_values() #データ型

output:

MasVnrArea      float64
GarageArea      float64
TotalBsmtSF     float64
BsmtFinSF1      float64
BsmtFinSF2      float64
GarageYrBlt     float64
BsmtFullBath    float64
BsmtHalfBath    float64
GarageCars      float64
BsmtUnfSF       float64
LotFrontage     float64
GarageType       object
KitchenQual      object
Alley            object
MasVnrType       object
MiscFeature      object
PoolQC           object
SaleType         object
MSZoning         object
GarageQual       object
Functional       object
GarageCond       object
FireplaceQu      object
Fence            object
Exterior2nd      object
Exterior1st      object
Electrical       object
BsmtQual         object
BsmtFinType2     object
BsmtFinType1     object
BsmtExposure     object
BsmtCond         object
GarageFinish     object
Utilities        object
dtype: object

学習データ、テストデータともにかなり欠損しています。
こういうときはパパッと欠損が多いカラムは削除してしまいたくなります。
ですが、その前に変数について詳しく説明しているドキュメントがKaggleにあげられているので、まずはそれを見てみましょう。
Kaggleからデータをダウンロードすると、「data_description.txt」というファイルも含まれていることに気がつきます。このファイルには、変数にどんなデータが格納されているのかが詳しく説明されています。
すると、大多数の欠損は情報がないことを意味するのではなく、欠損そのものが情報であることがわかります。
たとえば、最も欠損が多い、PoolQC(プールのクオリティ)をみてみましょう。
この変数の欠損はプールが住宅に存在しないことを意味しており、データの欠損そのものが情報となっています。
そのほかの変数(カテゴリカル変数)についても、欠損はその施設や設備が存在しないことを意味しているだけなのです。
また、数値型の変数についても、欠損は占有面積がゼロであることを意味しているだけであって、情報がないわけではありません。
したがって、カテゴリカル変数、数値型変数の欠損には以下の補完を行います。

• カテゴリカル変数の欠損：欠損を示す文字列’NA’を補完
• 数値型変数の欠損：0.0を補完

input:

# データ型に応じて欠損値を補完する
# floatの場合は0
# objectの場合は'NA'
na_float_cols = alldata[na_col_list].dtypes[alldata[na_col_list].dtypes=='float64'].index.tolist() #float64
na_obj_cols = alldata[na_col_list].dtypes[alldata[na_col_list].dtypes=='object'].index.tolist() #object
# float64型で欠損している場合は0を代入
for na_float_col in na_float_cols:
    alldata.loc[alldata[na_float_col].isnull(),na_float_col] = 0.0
# object型で欠損している場合は'NA'を代入
for na_obj_col in na_obj_cols:
    alldata.loc[alldata[na_obj_col].isnull(),na_obj_col] = 'NA'

マージデータの欠損を確認し、全て補完されていることを確認します。
input:

# マージデータの欠損状況
alldata.isnull().sum()[alldata.isnull().sum()>0].sort_values(ascending=False)

output:

Series([], dtype: int64)

全ての欠損値が補完されていることを確認できました。

カテゴリカル変数をダミー化

機械学習の定石通り、カテゴリカル変数をダミー化します。
本来はEDAでカテゴリカル変数についてもSalePriceとの関係性を探るべきですが、今回は飛ばします。
input:

# カテゴリカル変数の特徴量をリスト化
cat_cols = alldata.dtypes[alldata.dtypes=='object'].index.tolist()
# 数値変数の特徴量をリスト化
num_cols = alldata.dtypes[alldata.dtypes!='object'].index.tolist()
# データ分割および提出時に必要なカラムをリスト化
other_cols = ['Id','WhatIsData']
# 余計な要素をリストから削除
cat_cols.remove('WhatIsData') #学習データ・テストデータ区別フラグ除去
num_cols.remove('Id') #Id削除
# カテゴリカル変数をダミー化
alldata_cat = pd.get_dummies(alldata[cat_cols])
# データ統合
all_data = pd.concat([alldata[other_cols],alldata[num_cols],alldata_cat],axis=1)

目的変数の分布変換

学習データのSalePrice(住宅価格)の分布を確認します。
欠損補完の箇所で、プールがない住宅がほとんどであることがわかりました。
これは裏を返せばプールがあるような豪邸がいくつか存在するということであり、住宅価格がかなり歪な分布になっているのでは？と想定されます。
input:

sns.distplot(train['SalePrice'])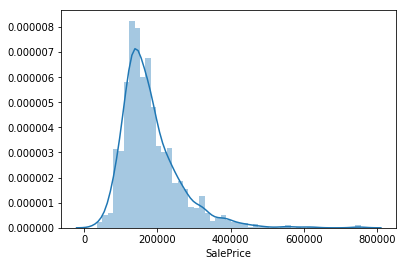

予想どおり、かなり右側に分布の裾野が広がっています。
対数変換をすることで正規分布に近づけます。
input:

sns.distplot(np.log(train['SalePrice']))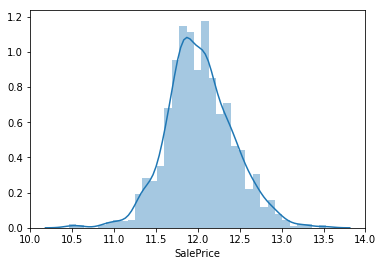

SalePrice(住宅価格)の分布が正規分布ライクになりました。
学習データの教師データにはこの対数変換後のSalePriceを用いることにします。

予測モデルの構築

今回は変数量がかなり多いため、係数に強力なペナルティをかけたいのでLasso回帰を使って予測モデルを構築します。
まず、学習データとテストデータにマージデータを分割します。
input:

# マージデータを学習データとテストデータに分割
train_ = all_data[all_data['WhatIsData']=='Train'].drop(['WhatIsData','Id'], axis=1).reset_index(drop=True)
test_ = all_data[all_data['WhatIsData']=='Test'].drop(['WhatIsData','SalePrice'], axis=1).reset_index(drop=True)
# 学習データ内の分割
train_x = train_.drop('SalePrice',axis=1)
train_y = np.log(train_['SalePrice'])
# テストデータ内の分割
test_id = test_['Id']
test_data = test_.drop('Id',axis=1)

基本的には数値変数に対しては標準化を施したうえでLasso回帰モデルを学習させます。
pipelineを使ってお手軽に前処理を施し、最適なLassoパラメータを探していきます。
input:

scaler = StandardScaler()  #スケーリング
param_grid = [0.001, 0.01, 0.1, 1.0, 10.0,100.0,1000.0] #パラメータグリッド
cnt = 0
for alpha in param_grid:
    ls = Lasso(alpha=alpha) #Lasso回帰モデル
    pipeline = make_pipeline(scaler, ls) #パイプライン生成
    X_train, X_test, y_train, y_test = train_test_split(train_x, train_y, test_size=0.3, random_state=0)
    pipeline.fit(X_train,y_train)
    train_rmse = np.sqrt(mean_squared_error(y_train, pipeline.predict(X_train)))
    test_rmse = np.sqrt(mean_squared_error(y_test, pipeline.predict(X_test)))
    if cnt == 0:
        best_score = test_rmse
        best_estimator = pipeline
        best_param = alpha
    elif best_score > test_rmse:
        best_score = test_rmse
        best_estimator = pipeline
        best_param = alpha
    else:
        pass
    cnt = cnt + 1
    
print('alpha : ' + str(best_param))
print('test score is : ' +str(best_score))

output:

alpha : 0.01
test score is : 0.180736908721

Lassoのパラメータα=0.01のときに汎化性能が0.18になることがわかりました。
ちなみに汎化性能は予測結果および教師データに自然対数をかけたものに対し、RMSE(root mean square error)を使って算出しています。
今回はこの予測モデルを使ってKaggleに提出します。

モデルの検証

学習したモデルが実際に教師データにどれくらい近似できているのかを検証してみます。
横軸が教師データ、縦軸が予測結果としてデータを散布します。
input:

plt.subplots_adjust(wspace=0.4)
plt.subplot(121)
plt.scatter(np.exp(y_train),np.exp(best_estimator.predict(X_train)))
plt.subplot(122)
plt.scatter(np.exp(y_test),np.exp(best_estimator.predict(X_test)))

output: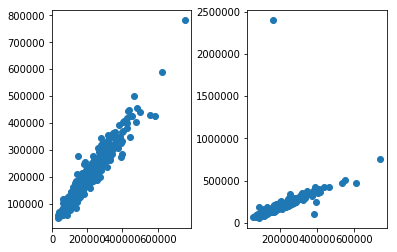

左が学習データ、右がテストデータになります。
学習データに対してはそこそこフィットしてますが、テストデータにはフィットしていないようです。
外れ値、過学習、特徴量エンジニアリング不足などなど課題は山積ですが、いったん先へ進みます。

予測結果の提出

最後に学習データ全体を使って予測モデルを再構築して予測結果を出力します。
ここで予測結果のSalePrice(住宅価格)は対数をとった値なので、最終的にはexponentialをかけてあげる必要があります。
input:

# 提出用データ生成
# test_id
ls = Lasso(alpha = 0.01)
pipeline = make_pipeline(scaler, ls)
pipeline.fit(train_x,train_y)
test_SalePrice = pd.DataFrame(np.exp(pipeline.predict(test_data)),columns=['SalePrice'])
test_Id = pd.DataFrame(test_id,columns=['Id'])
pd.concat([test_Id, test_SalePrice],axis=1).to_csv('../output/output.csv',index=False)

提出できました！