タイタニック号の乗客の生存予測～Kaggleに挑戦（その３）

2017.11.26
Kaggle
Titanic

3度目のチャレンジです。

今回は、ロジスティック回帰分析ではなく、機械学習の一つであるランダムフォレストを使ってタイタニック号の乗客の生存予測をします。

また、新たにFamilySize（家族数）とCabin（部屋番号）を説明変数に入れてモデルを作っています。

さて、スコアは伸びるのでしょうか？

1. FamilySize（家族数）と生存の関係
2. Cabin（部屋番号）と生存の関係
3. 予測モデル構築と評価
4. Kaggleへ提出

FamilySize（家族数）と生存の関係

推測ですが、タイタニック号の沈没事故において、家族は一緒になって行動していたと考えられます。

従って、家族全員が生存、あるいは全員が死亡したケースが多そうです。

実際に学習用データを確認してみます。

FamilySize（家族数）は既存の変数であるSibSp（兄弟、配偶者の数）とParch（両親、子供の数）によって以下の式で算出できます。

$$ FamilySize = SibSp + Parch + 1 $$

# 学習用データの読み込み
titanic_original <- read.csv("train.csv", stringsAsFactors=F, na.strings=(c("NA", "")))
# FamirySizeの追加
titanic_original <- cbind(titanic_original,titanic_original$SibSp+titanic_original$Parch+1)
colnames(titanic_original)[13] <- "FamilySize"
# FamilySizeごとの生存率
aggregate(x=list(value=titanic_original$Survived),by=list(keycol=titanic_original$FamilySize),FUN=mean)

出力結果

  keycol     value
1      1 0.3041045
2      2 0.5527950
3      3 0.5784314
4      4 0.7241379
5      5 0.2000000
6      6 0.1363636
7      7 0.3333333
8      8 0.0000000
9     11 0.0000000

FamilySize（家族数）が大きいほど、生存率が低そうですね。

5人以上の家族で乗船していた場合は、かなりの確率で死亡しています。

従って、FamilySize（家族数）はSurvived（生存）と関係がありあそうなので、説明変数として追加します。

Cabin（部屋番号）と生存の関係

Cabin（部屋番号）は1回目の投稿で調べた通り、欠損値が多かったため、今までは説明変数として利用するのを避けてきました。

キヨシの命題

タイタニック号の乗客の生存予測～Kaggleに挑戦（その１）

http://yolo-kiyoshi.com/2017/11/15/post-499/

だんだん冬が近づいてきましたね。そろそろシャツ1枚で外出するのは、世間体的に宜しくないシーズンとなってまいりました。さて、今回はKaggleという統計学を学んだ者にとっては胸が熱くなるようなサービスがあったので、統計解析手法の復習もかねてチャレンジしてみようと思います！（まずはKaggleにアプライすることをゴールにしています、、、）お題はタイタニック号の乗客の生存予測です。タイタニック号の沈没事故は皆さん映画で良くご存知だと思いますので、説明は省略します。当時の乗客のデータを使って、どんな乗客なら生存し...

しかし、調べてみると、Cabin（部屋番号）の頭文字に応じて部屋の階層が異なっていたようです。

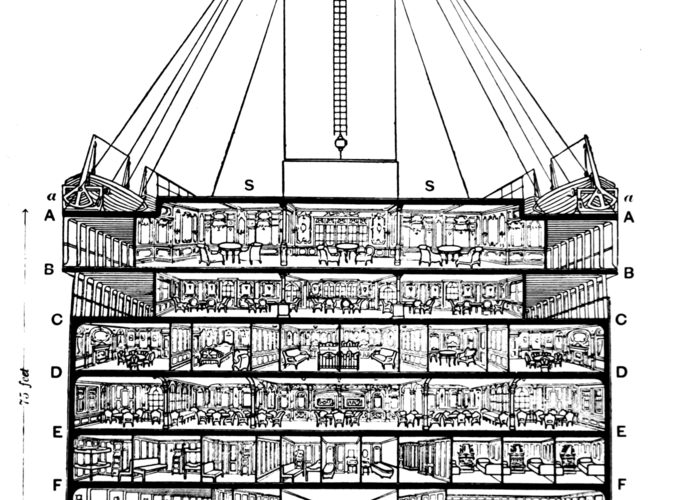
画像は、タイタニック号の断面図です。

横に振られているアルファベットは、Cabin（部屋番号）の頭文字となっています。

デッキに近い階層から順に、A、B、C...と振られていますね。

Kaggleのフォーラムでも以下のような記事があったので、参考になります。

www.kaggle.com

Titanic: Machine Learning from Disaster

https://www.kaggle.com/c/titanic/discussion/4693

Start here! Predict survival on the Titanic and get familiar with ML basics

救命ボートはデッキにあり、部屋がデッキに近い階層だった人のほうが生存したのではという推測ができます。

実際に学習用データを確認してみます。

# Cabinの頭文字を取得
titanic_original$Cabin <- ifelse(!is.na(titanic_original$Cabin),substr(titanic_original$Cabin,1,1),"U")  
# Cabinごとの生存率
aggregate(x=list(value=titanic_original$Survived),by=list(keycol=titanic_original$Cabin),FUN=mean)

出力結果

  keycol     value
1      A 0.4666667
2      B 0.7446809
3      C 0.5932203
4      D 0.7575758
5      E 0.7500000
6      F 0.6153846
7      G 0.5000000
8      T 0.0000000
9      U 0.2998544

Uは欠損値を意味しています。

欠損値になっている人の生存率が低いですね。

Aの乗客の生存率が低いのが気になりますが、一応これも説明変数として追加してみましょう。

予測モデル構築と評価

今回は複数モデルを作成し、学習用データでの予測制度が最も優れているモデルを採用することにしました。

# randomForestパッケージのインストール
install.packages("randomForest")

# 学習用データの読み込み
titanic_original <- read.csv("train.csv", stringsAsFactors=F, na.strings=(c("NA", "")))
# 学習用データ加工
name_honorific <- character(length(titanic_original$Name))

for(i in 1:length(titanic_original$Name)){
    # ","で文字列分割
    name_honorific[i] <- strsplit(strsplit(titanic_original$Name,", ")[[i]][2],"\\.")[[1]][1]
}

# 学習用データのNameを敬称で上書き
titanic_original$Name <- name_honorific

# 学習用データのAgeの欠損値を補完
titanic_original$Age <- ifelse(is.na(titanic_original$Age)
                           ,ifelse(titanic_original$Name == "Capt",70,
                            ifelse(titanic_original$Name == "Col",58,
                            ifelse(titanic_original$Name == "Don",40,
                            ifelse(titanic_original$Name == "Dr",42,
                            ifelse(titanic_original$Name == "Jonkheer",38,
                            ifelse(titanic_original$Name == "Lady",48,
                            ifelse(titanic_original$Name == "Major",48.5,
                            ifelse(titanic_original$Name == "Master",4.574166667,
                            ifelse(titanic_original$Name == "Miss",21.7739726,
                            ifelse(titanic_original$Name == "Mlle",24,
                            ifelse(titanic_original$Name == "Mme",24,
                            ifelse(titanic_original$Name == "Mr",32.36809045,
                            ifelse(titanic_original$Name == "Mrs",35.89814815,
                            ifelse(titanic_original$Name == "Ms",28,
                            ifelse(titanic_original$Name == "Rev",43.16666667,
                            ifelse(titanic_original$Name == "Sir",49,33))))))))))))))))
                           ,titanic_original$Age)
                           
# Cabinの頭文字を取得
titanic_original$Cabin <- ifelse(!is.na(titanic_original$Cabin),substr(titanic_original$Cabin,1,1),"U")                
titanic_original <- titanic_original[!titanic_original$Cabin=="T",]
# Levelsの更新（強制）
titanic_original$Cabin <- as.factor(as.character(titanic_original$Cabin))

# FamirySizeの追加
titanic_original <- cbind(titanic_original,titanic_original$SibSp+titanic_original$Parch+1)
colnames(titanic_original)[13] <- "FamilySize"
# AloneFlgの追加

# PassengerID、Ticketの除外
titanic_omit_vari <- titanic_original[,c(2,3,5:8,10:13)]
# NAを除外
titanic_na_omit <- na.omit(titanic_omit_vari)
# Sex（性別）の置き換え
# female:0,male:1
titanic_na_omit[,3] <- ifelse(titanic_na_omit[,3]=="female",0,1)
titanic_na_omit[,3] <- as.factor(titanic_na_omit[,3])
# Embarked（乗船した港）の置き換え
# C:0,Q:1,S:2
titanic_na_omit[,9] <- ifelse(titanic_na_omit[,9]=="C",0,ifelse(titanic_na_omit[,9]=="Q",1,2))
titanic_na_omit[,9] <- as.factor(titanic_na_omit[,9])
titanic_na_omit$Survived <- as.factor(titanic_na_omit$Survived)

# データをattach
attach(titanic_na_omit)
# ランダムフォレスト
library("randomForest")

# 予測モデル構築
model0 <- randomForest(Survived~., data=titanic_na_omit)
model1 <- randomForest(Survived~Pclass+Sex+Age+Cabin+Fare, data=titanic_na_omit)
model2 <- randomForest(Survived~Pclass+Sex+Age+SibSp+Cabin+Fare, data=titanic_na_omit)
model3 <- randomForest(Survived~Pclass+Sex+Age+SibSp+Fare, data=titanic_na_omit)
model4 <- randomForest(Survived~Pclass+Sex+Age+Fare+FamilySize, data=titanic_na_omit)
model5 <- randomForest(Survived~Pclass+Sex+Age+Fare+Cabin+FamilySize, data=titanic_na_omit)
model6 <- randomForest(Survived~Pclass+Sex+Age+Fare+Cabin, data=titanic_na_omit)

各モデルのサマリを確認します。

> model1

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + Cabin +      Fare, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 17.34%
Confusion matrix:
    0   1 class.error
0 491  57   0.1040146
1  97 243   0.2852941
> model2

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + SibSp +      Cabin + Fare, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 17.45%
Confusion matrix:
    0   1 class.error
0 488  60   0.1094891
1  95 245   0.2794118
> model3

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + SibSp +      Fare, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 17.91%
Confusion matrix:
    0   1 class.error
0 485  63   0.1149635
1  96 244   0.2823529
> model4

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + Fare +      FamilySize, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 16.67%
Confusion matrix:
    0   1 class.error
0 488  60   0.1094891
1  88 252   0.2588235
> model5

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + Fare +      Cabin + FamilySize, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 17.12%
Confusion matrix:
    0   1 class.error
0 485  63   0.1149635
1  89 251   0.2617647
> model6

Call:
 randomForest(formula = Survived ~ Pclass + Sex + Age + Fare +      Cabin, data = titanic_na_omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 17.23%
Confusion matrix:
    0   1 class.error
0 496  52  0.09489051
1 101 239  0.29705882

model4の予測精度が最も良いので、こちらを使って予測します。

せっかく追加したCabin（部屋番号）が説明変数に入っていませんが、予測精度が良いので仕方がありませんね。

Kaggleへ提出

以下のコードによりテストデータに予測モデルmodel4をあてはめ、予測結果を出力します。

# テストデータの読み込み
titanic_test <- read.csv("test.csv", stringsAsFactors=F, na.strings=(c("NA", "")))

# テストデータのFarの欠損値を補完
fare_med <- median(na.omit(titanic_test$Fare))
titanic_test$Fare <- ifelse(is.na(titanic_test$Fare),fare_med,titanic_test$Fare)

name_honorific <- character(length(titanic_test$Name))

for(i in 1:length(titanic_test$Name)){
    # ","で文字列分割
    name_honorific[i] <- strsplit(strsplit(titanic_test$Name,", ")[[i]][2],"\\.")[[1]][1]
}

# テストデータのNameを敬称で上書き
titanic_test$Name <- name_honorific

# テストデータのAgeの欠損値を補完
titanic_test$Age <- ifelse(is.na(titanic_test$Age)
                           ,ifelse(titanic_test$Name == "Capt",70,
                            ifelse(titanic_test$Name == "Col",58,
                            ifelse(titanic_test$Name == "Don",40,
                            ifelse(titanic_test$Name == "Dr",42,
                            ifelse(titanic_test$Name == "Jonkheer",38,
                            ifelse(titanic_test$Name == "Lady",48,
                            ifelse(titanic_test$Name == "Major",48.5,
                            ifelse(titanic_test$Name == "Master",4.574166667,
                            ifelse(titanic_test$Name == "Miss",21.7739726,
                            ifelse(titanic_test$Name == "Mlle",24,
                            ifelse(titanic_test$Name == "Mme",24,
                            ifelse(titanic_test$Name == "Mr",32.36809045,
                            ifelse(titanic_test$Name == "Mrs",35.89814815,
                            ifelse(titanic_test$Name == "Ms",28,
                            ifelse(titanic_test$Name == "Rev",43.16666667,
                            ifelse(titanic_test$Name == "Sir",49,33))))))))))))))))
                           ,titanic_test$Age)

titanic_test$Sex <- ifelse(titanic_test$Sex=="female",0,1)
titanic_test$Sex <- as.factor(titanic_test$Sex)
# Cabinの頭文字を取得
titanic_test$Cabin <- ifelse(!is.na(titanic_test$Cabin),substr(titanic_test$Cabin,1,1),"U")
titanic_test$Cabin <- as.factor(titanic_test$Cabin)

# FamirySizeの追加
titanic_test <- cbind(titanic_test,titanic_test$SibSp+titanic_test$Parch+1)
colnames(titanic_test)[12] <- "FamilySize"

# 予測モデルをテストデータにあてはめ
# 生存確率0.5以上なら生存:1、それ以外は死亡:0
test_result4 = predict(model4 titanic_test)
# PassengerId（乗客ID）を予測結果に列結合
output4 <- cbind(titanic_test$PassengerId,as.matrix(test_result4))
colnames(output4) <- c("PassengerId","Survived")
write.csv(output4,file="pred4.csv", row.names=FALSE)

さてさて予測結果は、、、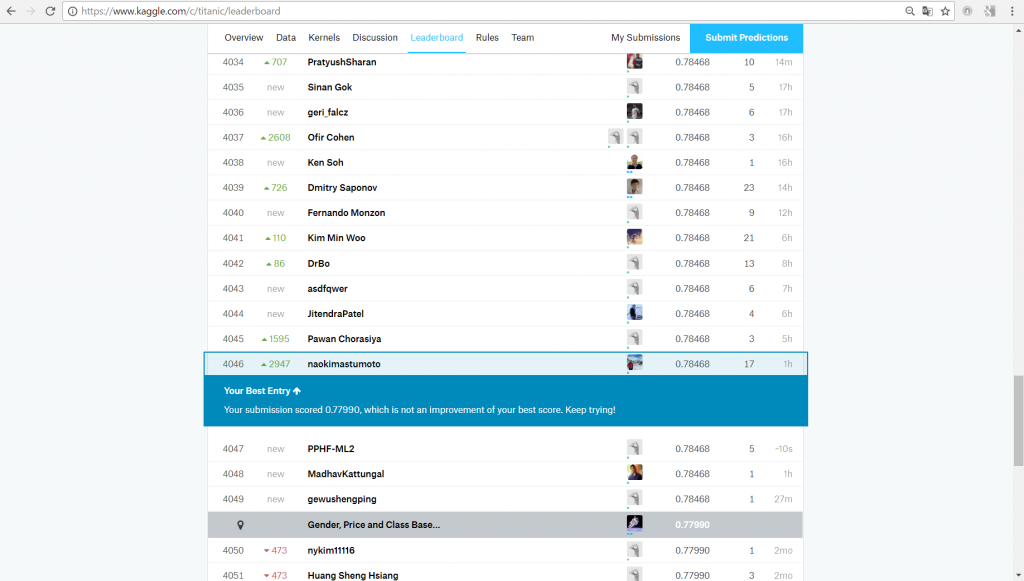

正答率は78.468%で、9,207人中4,046位でした。
前回よりも正答率は2.87%上昇、3755位ランクアップ。
目覚ましい進歩ですね！

一旦、予測に使ってきた手法を整理する記事を書きましょうか。

前の記事

タイタニック号の乗客の生存予測～Kaggleに挑戦（その２） 2017.11.19
次の記事

『ビッグデータを活かすデータサイエンス -クロス集計から機械学習までのビジネス活用事例』を読んだ感想 2017.11.28