タイタニック号の乗客の生存予測~Kaggleに挑戦(その1)

だんだん冬が近づいてきましたね。
そろそろシャツ1枚で外出するのは、世間体的に宜しくないシーズンとなってまいりました。
さて、今回はKaggleという統計学を学んだ者にとっては胸が熱くなるようなサービスがあったので、統計解析手法の復習もかねてチャレンジしてみようと思います!
(まずはKaggleにアプライすることをゴールにしています、、、)
お題はタイタニック号の乗客の生存予測です。
タイタニック号の沈没事故は皆さん映画で良くご存知だと思いますので、説明は省略します。
当時の乗客のデータを使って、どんな乗客なら生存し、または死亡したのかを解析し、予測モデルを構築していきます。
以下は本投稿以降でのKaggle titanic tutorialへの取り組みになります。
※統計解析言語Rを使っています。
Kaggleとは
一言でいえば、世界中のデータサイエンティストたちが、課題のデータを分析し、いかに最適なモデルを作れるかを競い合うサービスです。
以下は、wikipediaからの引用です。
Kaggleは企業や研究者がデータを投稿し、世界中の統計家やデータ分析家がその最適モデルを競い合う、予測モデリング及び分析手法関連プラットフォーム及びその運営会社である。
今回は、Kaggleの中でもチュートリアル的な課題である、タイタニック号の乗客の生存予測をやってみます!
タイタニック号の乗客データ
データの概要
以下から課題となっているタイタニックの乗客データをダウンロードできます。
ダウンロードできるデータは次の2つです。
- 学習用データ(予測モデルの構築に使用。乗客の生存情報もあり。)
- テストデータ(予測モデルの当てはめ用。乗客の生存情報なし。)
学習用データとしてKaggleで与えられている、タイタニック号の乗客のデータ項目は以下になります。
| 項目 | 説明 |
|---|---|
| PassengerID | 乗客ID(Kaggleが勝手につけたID) |
| Survived | 生存結果 (1: 生存, 2: 死亡) |
| Pclass | 乗客の階級(階級は1、2、3の順) |
| Name | 乗客の名前 |
| Sex | 性別 |
| Age | 年齢 |
| SibSp | 兄弟、配偶者の数 |
| Parch | 両親、子供の数 |
| Ticket | チケット番号 |
| Fare | 乗船料金 |
| Cabin | 部屋番号 |
| Embarked | 乗船した港(Cherbourg、Queenstown、Southampton) |
Rで学習用データを読み込み、欠損値を確認してみましょう。
(ここでは、空白も欠損値としています。)
input:
# 学習用データの読み込み
titanic_original <- read.csv("train.csv", stringsAsFactors=F, na.strings=(c("NA", "")))
# 学習用データの要約
apply(is.na(titanic_original), 2, sum)出力結果は以下になりました。
output:
PassengerId 0 Survived 0 Pclass 0 Name 0 Sex 0 Age 177 SibSp 0 Parch 0 Ticket 0 Fare 0 Cabin 687 Embarked 2
Age(年齢)、Cabin(部屋番号)にかなり欠損値が含まれていることがわかります。
データの加工
まずは乗客の生存に影響がなさそうな変数を除外していきましょう。
解析対象の変数が少ないほうがデータを見やすくなります。
以下の変数は乗客の生存に影響しなさそうなので除外します。
- PassengerID(乗客ID)
- Name(名前)
- Ticket(チケット番号)
- Cabin(部屋番号)
input:
# PassengerID、Ticket、Cabinの除外
titanic_omit_vari <- titanic_original[,c(2,3,5:8,10,12)]
# 変数の表示
names(titanic_omit_vari)output:
[1] "Survived" "Pclass" "Sex" "Age" "SibSp" [6] "Parch" "Fare" "Embarked"
次に、Age(年齢)またはEmbarked(乗船した港)が欠損値となっているレコードを除外します。
(今回は欠損値を補完せず、単純に除外します。)
input:
# NAを除外
titanic_na_omit <- na.omit(titanic_omit_vari)これで、データからは欠損値が除外されました。
最後に、文字列をデータとしているSEX(性別)、Embarked(乗船した港)を数値に置き換えます。
# SEX(性別)の置き換え
# female:0,male:1
titanic_na_omit[,3] <- ifelse(titanic_na_omit[,3]=="female",0,1)
# Embarked(乗船した港)の置き換え
# C:0,Q:1,S:2
titanic_na_omit[,8] <- ifelse(titanic_na_omit[,8]=="C",0,ifelse(titanic_na_omit[,8]=="Q",1,2))これで一旦、データ加工は終了です。
乗客の生存と相関がありそうな変数
加工したデータの変数間の相関を見てましょう。
input:
cor(titanic_na_omit)output:
Survived Pclass Sex Age SibSp Parch Fare Embarked Survived 1.00000000 -0.35646159 -0.53676162 -0.08244587 -0.01552302 0.09526529 0.26609960 -0.18197934 Pclass -0.35646159 1.00000000 0.15082621 -0.36590186 0.06518706 0.02366612 -0.55289322 0.24414499 Sex -0.53676162 0.15082621 1.00000000 0.09903723 -0.10629611 -0.24954273 -0.18245683 0.10963900 Age -0.08244587 -0.36590186 0.09903723 1.00000000 -0.30735094 -0.18789649 0.09314252 -0.03256492 SibSp -0.01552302 0.06518706 -0.10629611 -0.30735094 1.00000000 0.38333753 0.13986049 0.03306447 Parch 0.09526529 0.02366612 -0.24954273 -0.18789649 0.38333753 1.00000000 0.20662367 0.01180289 Fare 0.26609960 -0.55289322 -0.18245683 0.09314252 0.13986049 0.20662367 1.00000000 -0.28351044 Embarked -0.18197934 0.24414499 0.10963900 -0.03256492 0.03306447 0.01180289 -0.28351044 1.00000000
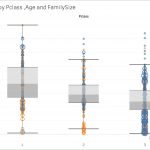
Survived(乗客の生存)との相関がありそうな変数は、Sex(性別)と、次いでPclass(乗客の階級)だと言えそうです。
映画『タイタニック』を観ていても、女性や階級の高い乗客が優先的に救命ボートに乗せられていましたし、感覚的には納得できます。
予測モデル構築
今回は、ロジスティック回帰分析によって予測モデルを構築してみます。
ロジスティック回帰は、予測したい変数が2値(成功or失敗、生存or死亡など)である場合に使われます。
以下はwikipediaからの引用です。
ロジスティック回帰(ロジスティックかいき、英: Logistic regression)は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種である。連結関数としてロジットを使用する一般化線形モデル (GLM) の一種でもある。1958年に David Cox が発表した[1]。確率の回帰であり、統計学の分類に主に使われる。医学や社会科学でもよく使われる。
では、glm関数を使って予測モデルを構築します。
input:
# データをattach
attach(titanic_na_omit)
# ロジスティック回帰モデル作成
glm_result <- glm(Survived~., family="binomial", data=titanic_na_omit)
# 回帰係数の確認
summary(glm_result)output:
Call:
glm(formula = Survived ~ ., family = "binomial", data = titanic_na_omit)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.7289 -0.6462 -0.3831 0.6296 2.4560
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.603225 0.631349 8.875 < 2e-16 ***
Pclass -1.221322 0.163519 -7.469 8.08e-14 ***
Sex -2.614396 0.220042 -11.881 < 2e-16 ***
Age -0.043463 0.008208 -5.295 1.19e-07 ***
SibSp -0.360044 0.127462 -2.825 0.00473 **
Parch -0.056259 0.123288 -0.456 0.64816
Fare 0.001472 0.002522 0.584 0.55945
Embarked -0.173286 0.132748 -1.305 0.19177
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 960.9 on 711 degrees of freedom
Residual deviance: 633.6 on 704 degrees of freedom
AIC: 649.6
Number of Fisher Scoring iterations: 5Parch(両親、子供の数)、Fare(乗船料金)、Embarked(乗船した港)は予測モデルの説明変数としては相応しくなさそうなので、除外して再度モデルを構築します。
input:
# 変数を絞ってロジスティック回帰モデル作成
glm_result <- glm(Survived~Pclass+Sex+Age+SibSp, family="binomial", data=titanic_na_omit)
# 回帰係数の確認
summary(glm_result)output:
Call:
glm(formula = Survived ~ Pclass + Sex + Age + SibSp, family = "binomial",
data = titanic_na_omit)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.7694 -0.6496 -0.3839 0.6298 2.4585
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.59083 0.54342 10.288 < 2e-16 ***
Pclass -1.31392 0.14091 -9.324 < 2e-16 ***
Sex -2.61477 0.21473 -12.177 < 2e-16 ***
Age -0.04459 0.00817 -5.457 4.83e-08 ***
SibSp -0.37465 0.12093 -3.098 0.00195 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 960.90 on 711 degrees of freedom
Residual deviance: 636.18 on 707 degrees of freedom
AIC: 646.18
Number of Fisher Scoring iterations: 5更新したモデルは、更新前のモデルに比べてAIC(赤池情報量基準)がしっかり減少しているので、より最適な予測モデルになったと言えます。
\( p \) を生存する確率とすると、以下の予測モデル式となります。
$$ \log \frac{p}{1-p} = 5.59083 -1.31392 \times Pclass -2.61477 \times Sex \\
-0.04459 \times Age -0.37465 \times SibSp $$
予測結果
テストデータを読み込み、テストデータの欠損値を確認します。
input:
# テストデータの読み込み
titanic_test <- read.csv("test.csv", stringsAsFactors=F, na.strings=(c("NA", "")))output:
PassengerId 0 Survived 0 Pclass 0 Name 0 Sex 0 Age 86 SibSp 0 Parch 0 Ticket 0 Fare 1 Cabin 327 Embarked 0
予測モデルの説明変数であるAge(年齢)に、86も欠損値が含まれています。
しかし、学習データを加工したときとは異なり、Age(年齢)の欠損値を除外してはいけません。
Age(年齢)は予測モデルの説明変数であるため、何らかの数値で補完してあげる必要があります。
今回は簡単に、学習モデルにおけるAge(年齢)のMedian(中央値)を使います。
input:
# 学習モデルにおけるAgeのmedianを計算
median(na.omit(titanic_original$Age))output:
[1] 28
従って、学習データのAge(年齢)の中央値は28であり、この数値を使って、テストデータの欠損値を補完します。
input:
# テストデータのAgeの欠損値を補完
titanic_test$Age <- ifelse(is.na(titanic_test$Age),28,titanic_test$Age)これで、テストデータのAge(年齢)の欠損値の補完ができました。
次に、学習データを加工した際と同様に、文字列をデータとしているSex(性別)を数値に置き換えます。
input:
# Sex(性別)の置き換え
# female:0,male:1
titanic_test$Sex <- ifelse(titanic_test$Sex=="female",0,1)テストデータの加工が完了したので、最後は学習データで構築した予測モデルをテストデータにあてはめ、生存を予測します。
input:
# 予測モデルをテストデータにあてはめ
# 生存確率0.5以上なら生存:1、それ以外は死亡:0
test_result <- ifelse(predict(glm_result,newdata=titanic_test,type="response")>=0.5,1,0)
# PassengerId(乗客ID)を予測結果に列結合
output <- cbind(titanic_test$PassengerId,test_result)
# 先頭から数行を確認
head(output)output:
test_result 1 892 0 2 893 0 3 894 0 4 895 0 5 896 1 6 897 0
以上が予測結果となります。
Kaggleへ予測結果を提出
タイタニック号の乗客の生存予測結果をKaggleへ提出します。
以下のページで、提出フォーマットを説明しています。
You should submit a csv file with exactly 418 entries plus a header row. Your submission will show an error if you have extra columns (beyond PassengerId and Survived) or rows.
The file should have exactly 2 columns:
・PassengerId (sorted in any order)
・Survived (contains your binary predictions: 1 for survived, 0 for deceased)
要は、csv形式で、ヘッダーにPassengerIdとSurvivedを入れて、418行のデータで提出しなさいということです。
Kaggleへログインすると「My Submission」タブが表示されるので、それをクリックし、csvファイルをアップロードします。
予測結果を提出フォーマットに整形し、Kaggleへ提出した結果。
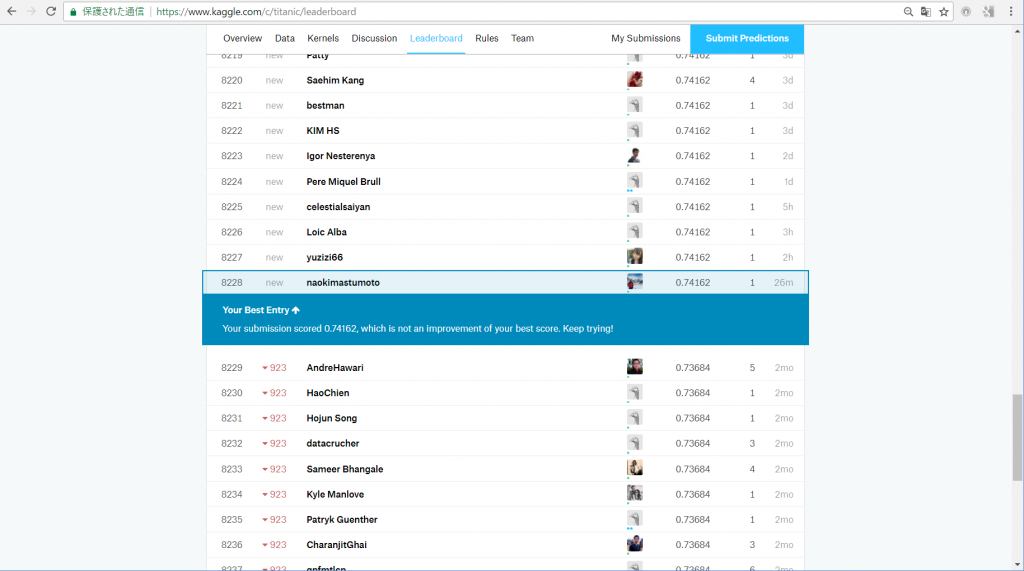
正答率は74.162%で、9,207人中8,245位でした。
クソみたいな順位ですね笑
必要最低限の解析しかしていないから当然ではありますが。
ただ、ほんの0.1%でも正答率を改善することで格段に順位が上がります。
それだけ、上位はひしめき合っているということです。
まとめ
次回のチャレンジでは以下を改善すれば順位が上がるはずです。
- Age(年齢)の欠損値補完に一工夫入れる(他の変量で予測できるはず)
- 乗客の生存に影響がある因子を考慮した予測モデルを構築する
- アンサンブル機械学習を導入する
今回のチャレンジを通して、Kaggleへのアプライの流れを理解できたので、次は本腰を入れてやってみようと思います!
- 前の記事

深夜に浅草寺へ行ってみよう! 2017.11.06
- 次の記事

『怖い絵(角川文庫)』を読んだ感想 2017.11.18