タイタニック号の乗客の生存予測〜80%以上の予測精度を超える方法(探索的データ解析編)
今さらですが、ついにKaggleのタイタニック チュートリアル(titanic tutorial)でAccuracy80%を達成できました。
※過去に3つほどtitanic tutorialについての記事を書いています。titanic tutorialって何?っていう方は以下に詳しくまとめていますのでご参照ください。
どうやってAccuracy80%を超えられたのかを、「探索的データ解析編」と「モデル構築&推論編」に分けて備忘録的にまとめます。
(なので、今回は「探索編」をまとめます。)
モデル構築&推論編はこちらです。
まず、予測モデルの構築に必要な特徴量を見極めるために、改めて探索的データ解析(EDA)を実施します。
※EDAの目的はきれいなグラフを作って満足することではなく、モデル構築に必要なデータを見極めていくことです。
解析に使用する言語はPythonでバージョンは3.7です。
今回のEDAでは各説明変数ごとに次の分析していきます。
- Survived(生存)と説明変数の関係
予測モデル構築時に使用する特徴量を選定するため - 学習データとテストデータの分布
予測モデルの訓練に使うデータと予測に使うデータの分布に偏りがないかを事前に把握するため
環境準備
以下のディレクトリ構造で分析を進めていきます。
├── data │ ├── processed │ ├── raw │ │ ├── gender_submission.csv │ │ ├── test.csv │ │ └── train.csv │ └── submitted ├── docker-compose.yml ├── notebook │ └── eda.ipynb ├── poetry.lock └── pyproject.toml
Dockerコンテナ上で分析環境を構築しています。
notebookだけを観たいという方はコードをgitにあげておりますので、こちらをご覧ください。
データ準備
学習データとテストデータを読み込みます。
データはKaggleの以下のページからダウンロードできます。
ダウンロードしたtrain.csvとtest.csvをdata/raw配下におき、以下を実行します。
input:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
train_raw = pd.read_csv('../data/raw//train.csv') #学習データ
test_raw = pd.read_csv('../data/raw/test.csv') #テストデータ
print('The size of the train data:' + str(train_raw.shape))
print('The size of the test data:' + str(test_raw.shape))output:
The size of the train data:(891, 12) The size of the test data:(418, 11)
次に学習データとテストデータの分布を調べるために、データをマージします。
マージする前に学習データとテストデータに以下の処理をします。
- 学習データとテストデータを区別できるようにtrain_or_testカラムを追加
- テストデータにSurvivedカラムを追加
input:
# 学習データとテストデータのマージ
train_mid = train_raw.copy()
test_mid = test_raw.copy()
train_mid['train_or_test'] = 'train' #学習データフラグ
test_mid['train_or_test'] = 'test' #テストデータフラグ
test_mid['Survived'] = 9 #テストにSurvivedカラムを仮置き
alldata = pd.concat(
[
train_mid,
test_mid
],
sort=False,
axis=0
).reset_index(drop=True)探索的データ解析
データの準備が終わったので、ここからは各説明変数ごとにデータをみていきます。
ですが、その前に各説明変数とSurvived(生存)の関係を調べる上でベースラインとなる学習データ全体における生存率を確認しておきます。
input:
# 生存率のベースライン
train_raw['Survived'].mean() #学習データにおける生存率output:
0.3838383838383838
生きるか死ぬかの2パターンだから生存率は0.5と機械的に考えてしまいがちですが、学習データにおける生存率は約0.38です。
これから各説明変数と生存率の関係をみていくとき、この生存率0.38という数値が判断基準になります。
Pclass
PclassごとのSurvivedの平均(生存率)を算出します。
input:
# Pclass別の生存率
train_raw['Survived'].groupby(train_raw['Pclass']).mean()output:
Pclass 1 0.629630 2 0.472826 3 0.242363 Name: Survived, dtype: float64
ベースライン生存率が0.38だったので、Pclassと生存率には何らかの関係がありそうです。
Pclassごとの乗客数もみてみます。
# Pclass別の生存数カウント
sns.countplot(train_raw['Pclass'], hue=train_raw['Survived'])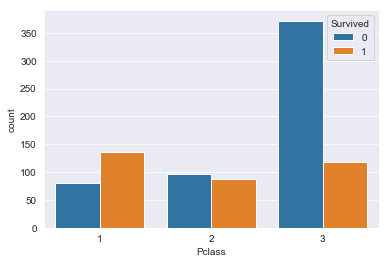
グラフからPclassが3の乗客に死亡者(Survived:0)が多いことがわかります。
次に学習データとテストデータの分布を確認します。
input:
# Pclassの分布
pd.crosstab(alldata['Pclass'],alldata['train_or_test'],normalize='columns')output:
WhatIsData Test Train Pclass 1 0.255981 0.242424 2 0.222488 0.206510 3 0.521531 0.551066
学習データとテストデータ間のPclassの乗客数の分布に大きな偏りはなさそうです。
Name
Name(乗客の名前)はSurvived(生存)とは関係がなさそうですが、いったん実データを眺めてみます。
input:
# Nameの確認
train_raw['Name'].head()output:
0 Braund, Mr. Owen Harris 1 Cumings, Mrs. John Bradley (Florence Briggs Th... 2 Heikkinen, Miss. Laina 3 Futrelle, Mrs. Jacques Heath (Lily May Peel) 4 Allen, Mr. William Henry Name: Name, dtype: object
Nameには文字通り乗客の名前が格納されています。
名前を眺めていると、真ん中に共通している部分があることがわかります。
英語表記の名前はfirst name, middle name, last nameで表現されていて、このmiddle nameの部分になんらかの情報が含まれていそうです。
いったんこのmiddle nameの部分を切り出してみます。
(middle nameはhonorific(敬称)と呼ばれるので、コードではhonorificと表記しています。)
input:
# 敬称(honorific)を抽出
train_raw['honorific'] = train_raw['Name'].map(lambda x: x.split(', ')[1].split('. ')[0])
train_raw['honorific'].value_counts() #敬称別のレコード数output:
Mr 517 Miss 182 Mrs 125 Master 40 Dr 7 Rev 6 Major 2 Col 2 Mlle 2 Capt 1 Mme 1 Jonkheer 1 Lady 1 Sir 1 Don 1 the Countess 1 Ms 1 Name: honorific, dtype: int64
Miss, Mrs, Masterが多くの乗客で共通しています。
次に学習データとテストデータの分布を確認します。
input:
# テストデータの敬称(honorific)を抽出
alldata['honorific'] = alldata['Name'].map(lambda x: x.split(', ')[1].split('. ')[0])
pd.crosstab(alldata['honorific'],alldata['train_or_test']) #敬称別のレコード数output:
WhatIsData Test Train honorific Capt 0 1 Col 2 2 Don 0 1 Dona 1 0 Dr 1 7 Jonkheer 0 1 Lady 0 1 Major 0 2 Master 21 40 Miss 78 182 Mlle 0 2 Mme 0 1 Mr 240 517 Mrs 72 125 Ms 1 1 Rev 2 6 Sir 0 1 the Countess 0 1
上記の結果を眺めてみると、テストデータにはなく学習データにしかないmiddle name(honorific)がちらほらと存在しています。
このようなデータは予測モデル構築の際には邪魔なデータになるので学習データから除外します。
その上で生存率を確認してみます。
例えば、学習データにしか存在しないCaptは、おそらく船長を表しているはずです。
船長は予想通り死亡しています。
テストデータに存在していないこのデータを学習データにいれることは、少なくともモデルをよくする方に働かないと考えます。
input:
# 学習データにしか現れない敬称を除外
only_train_honorific = ['Capt','Don','Jonkheer','Lady','Major','Mile','Mme','Sir','the Countess']
train_omit1 = train_raw[~train_raw['honorific'].isin(only_train_honorific) ].reset_index(drop=True)
# 敬称別の生存率とレコード数
train_omit1['Survived'].groupby(train_omit1['honorific']).agg(['mean','count'])output:
mean count honorific Col 0.500000 2 Dr 0.428571 7 Master 0.575000 40 Miss 0.697802 182 Mlle 1.000000 2 Mr 0.156673 517 Mrs 0.792000 125 Ms 1.000000 1 Rev 0.000000 6
ベースライン生存率0.38と比較すると、敬称(honorific)は生存と関係がありそうです。
Col, Dr, Mlle, Ms, Revのレコード数がわずかしかないため、統合します。
input:
train_omit1['honorific'].replace(['Col','Dr', 'Rev'], 'Rare',inplace=True) #少数派の敬称を統合
train_omit1['honorific'].replace('Mlle', 'Miss',inplace=True) #Missに統合
train_omit1['honorific'].replace('Ms', 'Miss',inplace=True) #Missに統合
# 敬称別の生存率
train_omit1['Survived'].groupby(train_omit1['honorific']).agg(['mean','count'])output:
mean count honorific Master 0.575000 40 Miss 0.702703 185 Mr 0.156673 517 Mrs 0.792000 125 Rare 0.266667 15
やはり敬称(honorific)は生存と関係がありそうです。
Fare
まずはFare(運賃)をSurvivedに分けて分布を確認します。
input:
# Fareの分布
sns.distplot(train_raw[train_raw['Survived']==1]['Fare'],kde=False,rug=False,bins=10,label='Survived')
sns.distplot(train_raw[train_raw['Survived']==0]['Fare'],kde=False,rug=False,bins=10,label='Death')
plt.legend()output: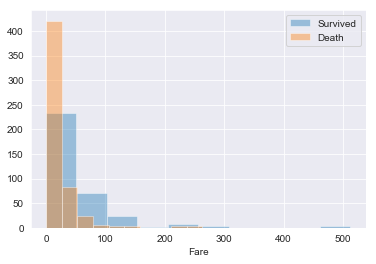
全体で見たときにFareが少ない乗客が大半で、かなり右に裾野が広がっていることがわかります。
Fareのskewness(歪度)を確認します。
input:
print("Skewness of Fare:", train_raw['Fare'].skew()) #Fareの歪度output:
Skewness of Fare: 4.78731651967
skewnessが大きい値となっていて分布が歪んでいるので、対数変換をして分布を修正します。
input:
# 分布が歪んでいるためFareを対数変換して再度分布を確認
sns.distplot(np.log1p(train_raw[train_raw['Survived']==1]['Fare']),kde=False,rug=False,bins=10,label='Survived')
sns.distplot(np.log1p(train_raw[train_raw['Survived']==0]['Fare']),kde=False,rug=False,bins=10,label='Death')
plt.legend()output: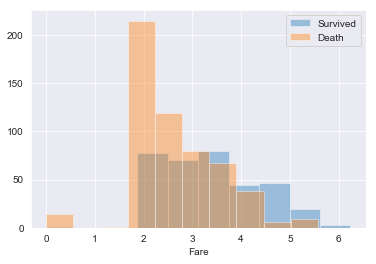
グラフをみると、少なくとも死亡者(Survived:0)に関してはSurvivedと関係がありそうです。
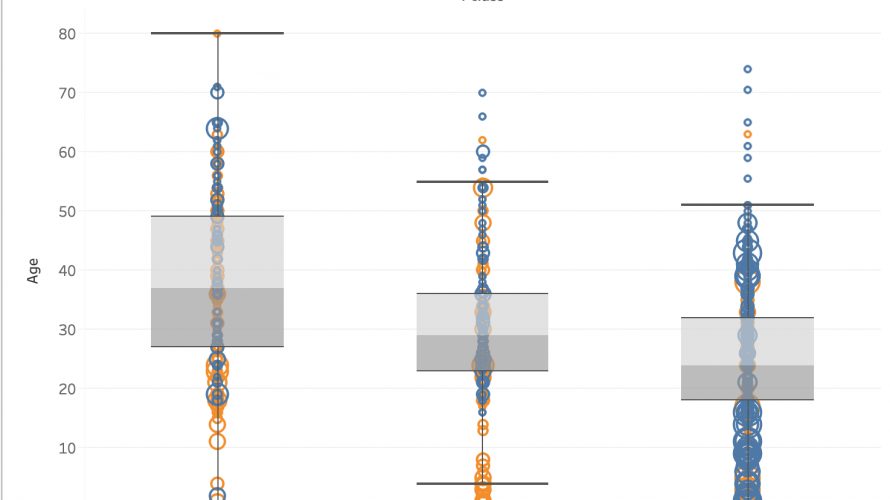
Age
Ageはそもそも欠損が多い変数です。
いたって素朴な想像ですが、年齢の欠損ってそもそも生存率に関係があるのでは?と思ったので、いったん欠損有無による生存率をみてみます。
Ageが欠損しているってことは死亡しているからそもそもデータが取れていないんじゃ?と思ったためです。
input:
# Ageの欠損有無による生存率差
train_raw['Survived'].groupby(train_raw['Age'].isnull()).mean()output:
Age False 0.406162 True 0.293785 Name: Survived, dtype: float64
う〜ん、これだと生存率に差があるかどうかはなかなか言いにくいかもしれません。
いったん欠損値を除外して分布をみてみます。
input:
# Ageの欠損を除外
train_age_omit = train_raw.dropna(subset=['Age'])
# Ageの分布
sns.distplot(train_age_omit[train_age_omit['Survived']==1]['Age'],kde=True,rug=False,bins=10,label='Survived') #生存者の分布
sns.distplot(train_age_omit[train_age_omit['Survived']==0]['Age'],kde=True,rug=False,bins=10,label='Death') #死者の分布
plt.legend()output: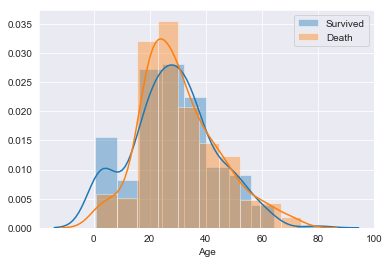
グラフを見ると、20歳以降の分布は生存、死亡ともに似通っていますが、0~20歳までの分布に差があります。
子供は生き残りやすかったと言えそうです。
FamilySize(Parch+Sibsp+1)
与えられたデータには存在しない、FamilySize(家族数)という変数を追加して分布を確認します。
input:
# 家族数 = Parch + SibSp + 1
train_raw['FamilySize'] = train_raw['Parch'] + train_raw['SibSp'] + 1 #学習データ
alldata['FamilySize'] = alldata['Parch'] + alldata['SibSp'] + 1 #ALLデータ
# 家族数ごとの分布を確認
sns.countplot(train_raw['FamilySize'],hue=train_raw['Survived'])output: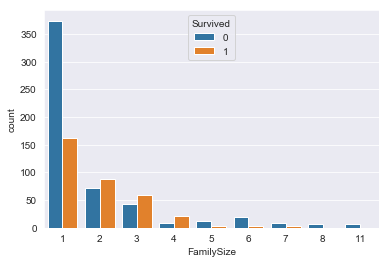
グラフを見ると、家族数:1(単身)は生存率が低く、家族数:2~4(小家族)は生存率が高く、それ以降はまた生存率が低いことがわかります。
FamilySizeと生存の間に線形関係がなさそうなのでビニング処理をします。
input:
# FamilySizeを離散化
train_raw['FamilySize_bin'] = 'big'
train_raw.loc[train_raw['FamilySize']==1,'FamilySize_bin'] = 'alone'
train_raw.loc[(train_raw['FamilySize']>=2) & (train_raw['FamilySize']<=4),'FamilySize_bin'] = 'small'
train_raw.loc[(train_raw['FamilySize']>=5) & (train_raw['FamilySize']<=7),'FamilySize_bin'] = 'mediam'
# FamilySizeを離散化したときの生存率
train_raw['Survived'].groupby(train_raw['FamilySize_bin']).mean()output:
FamilySize_bin alone 0.303538 big 0.000000 mediam 0.204082 small 0.578767 Name: Survived, dtype: float64
ビニング処理をしたFamilySizeは生存と関係がありそうです。
小さい家族は生存しやすく、大家族は生存しにくかったと言えます。
Cabin
Cabin(客室)を見ていきます。
この変数に関しては以前このブログでも考察をあげていますので詳しくは以下をご参照ください。
Cabinの頭文字は部屋がどの階層にあったのかを示すものなので、まずはCabinの頭文字ごとの生存率を確認します。
input:
# Cabinの頭文字
train_raw['Cabin_ini'] = train_raw['Cabin'].map(lambda x:str(x)[0])
alldata['Cabin_ini'] = alldata['Cabin'].map(lambda x:str(x)[0])
# Cabinの頭文字別の生存率とレコード数
train_raw['Survived'].groupby(train_raw['Cabin_ini']).agg(['mean','count'])output:
mean count Cabin_ini A 0.466667 15 B 0.744681 47 C 0.593220 59 D 0.757576 33 E 0.750000 32 F 0.615385 13 G 0.500000 4 T 0.000000 1 n 0.299854 687
Cabinの頭文字は生存率と何らかの関係がありそうです。
次に学習データとテストデータの分布を確認します。
input:
# Cabinの頭文字別のカウント数
pd.crosstab(alldata['Cabin_ini'],alldata['train_or_test'])output:
WhatIsData Test Train Cabin_ini A 7 15 B 18 47 C 35 59 D 13 33 E 9 32 F 8 13 G 1 4 T 0 1 n 327 687
Cabin:Tに関しては学習データにしか存在しないため、Tは予測モデル構築時には学習データから除外する方がよさそうです。
Ticket
最後にTicketを調べていきます。
まずはTicketにはどんなデータが入っているのかを確認します。
input:
train_raw['Ticket'].head()output:
0 A/5 21171 1 PC 17599 2 STON/O2. 3101282 3 113803 4 373450 Name: Ticket, dtype: object
Nameと違って規則性を見つけるのは難しそうです。先頭が英語あるいは数字の場合があるので、いったんTicketの1文字目に着目してデータをまとめてみます。
input:
train_raw['Survived'].groupby(train_raw['Ticket'].map(lambda x: str(x)[0])).agg(['mean','count'])output:
mean count Ticket 1 0.630137 146 2 0.464481 183 3 0.239203 301 4 0.200000 10 5 0.000000 3 6 0.166667 6 7 0.111111 9 8 0.000000 2 9 1.000000 1 A 0.068966 29 C 0.340426 47 F 0.571429 7 L 0.250000 4 P 0.646154 65 S 0.323077 65 W 0.153846 13
上記のデータをみてみると、Ticketの1文字目と生存には何らかの関係がありそうです。
学習データとテストデータ間の分布をみてみます。
input:
# 学習データとテストデータの分布を確認
pd.crosstab(alldata['Ticket'].map(lambda x: str(x)[0]),alldata['train_or_test'])output:
WhatIsData Test Train Ticket 1 64 146 2 95 183 3 128 301 4 1 10 5 0 3 6 3 6 7 4 9 8 0 2 9 1 1 A 13 29 C 30 47 F 6 7 L 1 4 P 33 65 S 33 65 W 6 13
学習データにしか存在していない項目がちらほらあります。
ただ、Ticketについては先頭の1文字目がどう言う意味を表すのかがよくわかりません。
ここで、発想を転換し、Ticketに重複カウントがないのかを調べてみます。
家族や友人同士でチケットを購入した場合、同一のチケット番号かあるいは末尾が少しだけ異なる番号になるのでは?と予想できるためです。
input:
# Ticketの頻度のヒストグラム
plt.hist(alldata.Ticket.value_counts())
plt.title('frequency of ticket')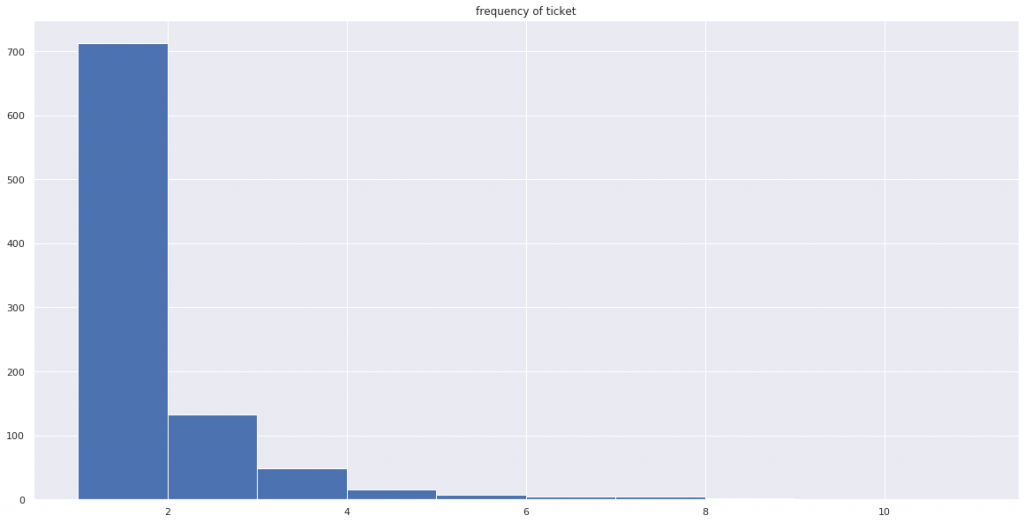
Ticketが重複している乗客がいくらか存在しているようです。
trainデータにおいて、このTicketの頻度と生存率の関係をみてみます。
input:
# Ticket頻度別の生存率
alldata.loc[:, 'TicketFreq'] = alldata.groupby(['Ticket'])['PassengerId'].transform('count')
alldata.query('train_or_test == "train"').groupby(['TicketFreq'])['Survived'].agg(['mean','count'])output:
mean count TicketFreq 1 0.270270 481 2 0.513812 181 3 0.653465 101 4 0.727273 44 5 0.333333 21 6 0.210526 19 7 0.208333 24 8 0.384615 13 11 0.000000 7
どうやら、Ticketの頻度と生存率は関係がありそうですね。
さて、次回はSurvivedに関係がありそうな特徴量を使って予測モデルの構築からKaggleへの予測結果の提出までを説明します。
- 前の記事
Tableauで始めるアドホック分析~SQLと関連づけてTableauの仕組みを理解する 2018.12.09
- 次の記事

住宅価格を予測する〜Kaggle House Priceチュートリアルに挑む 2018.12.17