切片が0の回帰モデルにおける決定係数の解釈

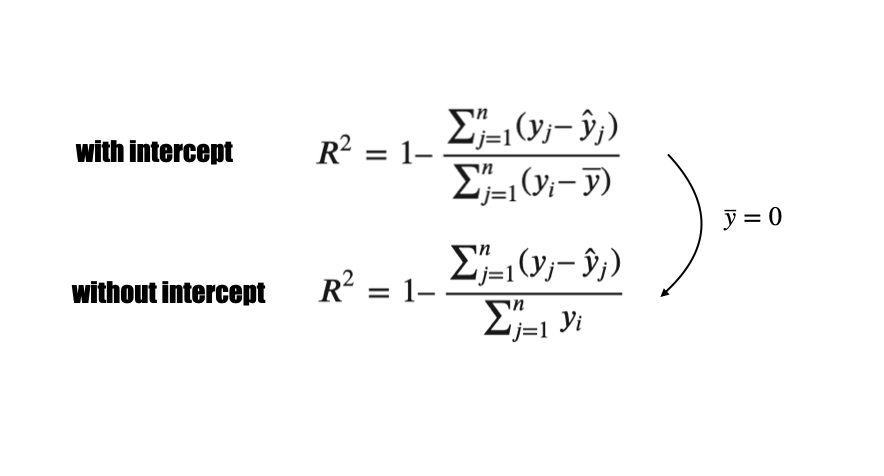
『Rで学ぶ確率統計学 多変量統計編』の「第３章　単回帰分析」を読んでいて、切片が0のとき（原点を通る）回帰モデルにおける決定係数について興味深い解釈がなされていたので、頭の整理としてまとめます。

なお、今回のテーマですが、残念ながら日本語の記事はほぼ存在しなかったものの、海外ではよく議論されているようです。

決定係数とは

決定係数は回帰モデルにおける当てはまりの良し悪しを判断するための指標で、以下で定義されます。
$$
R^2 = 1 – \frac{\sum_{j=1}^{n}(y_j – \hat{y}_j)}{\sum_{j=1}^{n}(y_i – \overline{y})}
$$

ここで、数式に用いられている記号は以下となります。

• \(y_j\): 観測値
• \(\hat{y}_j\): 予測値 \(\alpha + \beta x_j\)
• \(\overline{y}\): 観測値の平均値

決定係数は直線の当てはまりが良い場合は1に近い値となり、当てはまりが悪い場合は0に近い値になります。

切片が0の場合の決定係数の解釈

上記で述べた決定係数は、切片が存在する回帰モデルでは直線の当てはまり具合の指標として利用できますが、切片が0の回帰モデルではその意味が変わります。

説明のため、決定係数を再掲します。
$$
R^2 = 1 – \frac{\sum_{j=1}^{n}(y_j – \hat{y}_j)}{\sum_{j=1}^{n}(y_i – \overline{y})}
$$
右辺の2項目は定義上、残差（観測値と予測値の差）と全変動（観測値と観測値平均値）の比率となっています。
ですが、一度その定義を忘れて、分母・分子ともに予測値（\(y_j = \alpha + \beta x_j\)）の2つのパラメータ\(\alpha, \beta\)を自由に動かしたときの観測値との乖離を意味するものと捉えます。

そうすると、分母では既に2つのパラメータ\(\alpha, \beta\)が固定されていることになります。
（\(\alpha=\overline{y}, \beta = 0\)）

切片が存在するモデルでは、2つのパラメータ\(\alpha, \beta\)をどちらも自由に選べるという前提において、最小二乗法でパラメータを推定します。
もちろん、分母で固定されているパラメータである\(\alpha=\overline{y}, \beta = 0\)も「自由に選べる」対象に含まれます。

一方、切片が0の場合は、\(\alpha=0\) が前提として（\(\alpha\) を固定し、\(\beta\) だけを自由に選べる）、最小二乗法でパラメータを推定します。
このとき、\(\overline{y}\neq 0\) とすると、分母で固定している\(\alpha=\overline{y}, \beta = 0\) は分子における「自由に選べる」対象に含まれないことになります。
つまり、分母、分子でパラメータの探索範囲が重ならないのです。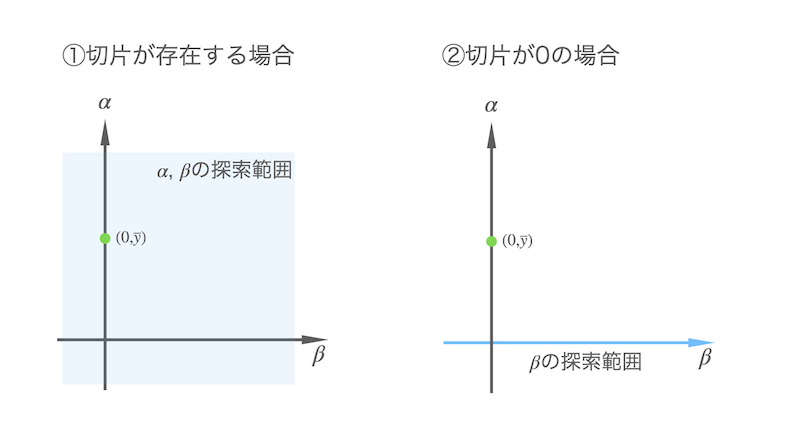

なお、\(\overline{y}=0\) であれば分母、分子のパラメータの探索範囲に重なりがあるため決定係数\(R^2\)を算出可能です。
したがって、切片が0の場合の決定係数\(R^2\)は以下で定義されます。
$$
R^2 = 1 – \frac{\sum_{j=1}^{n}(y_j – \hat{y}_j)}{\sum_{j=1}^{n}y_i}
$$

最後に

今回のテーマを理解するために参考資料で紹介している文献をいろいろと読みましたが、『Rで学ぶ確率統計学 多変量統計編』が一番分かりやすく書かれていると思いました。

参考資料

• 日本語で書かれた記事
• Regression through the Origin
• Rの公式FAQ