ランクがある2つのリストの相関係数の算出にAverage Precisionを導入する方法

2020.04.15
統計解析

最近、『A new rank correlation coefficient for information retrieval』という論文を読みました。
本論文では、ランクがある2つのリストにおける相関係数を算出するために、Average Precisionを利用することを提案しています。
従来、こういったランクがある2つのリストにおける相関係数としてはスピアマンの順位相関係数やケンドールの順位相関係数が使われています。
しかし、スピアマンの順位相関係数やケンドールの順位相関係数はランクの上位あるいは下位での誤りに対して等しくペナルティをかけてしまいます。
情報検索やレコメンドの観点では、上位のランクにおける誤りにより大きなペナルティがかかり、下位にいくに従ってペナルティを緩和させる方が自然です。
この論文ではそういった考え方に基づき、かかるペナルティの大きさが誤りがあるランクの位置に依存する $AP(Average\,Precision)$ をもとにした新たな順位相関係数を提案しています。

今回は、従来よく使われているスピアマンの順位相関係数、ケンドールの順位相関係数に加えて、この論文で提案されている $AP\,correlation$ も説明します。

1. スピアマンの順位相関係数
- 1.1. 定義
- 1.2. 実装例
2. ケンドールの順位相関係数
3. AP correlation
4. 指標比較
5. まとめ
6. 参考

スピアマンの順位相関係数

スピアマンの順位相関係数は、ピアソンの積率相関係数の定義をランクがある2つのリストに適用したものです。

定義

$$
r = 1 – \frac{6}{n^3 – n}\sum^n_{i=1}\left( R_i – R’_i \right)^2
$$

$n$ ：リストの長さ
$R_i$ ：リスト $R$ におけるアイテム $i$ のランク

実装例

Pythonでの実装例は以下になります。

def spearman_corr(list_1: list, list_2: list) -> float:
    """
    スピアマンの順位相関係数を算出するメソッド。

    Parameters
    -------
    list_1 : list
        ランクで昇順ソートされたアイテムのリスト。
    -------
    list_2 : list
        ランクで昇順ソートされたアイテムのリスト。

    Returns
    -------
    spearman_correlation : float
        スピアマンの順位相関係数
    
    """
    # リストのアイテムがkey、ランクがvalueのdict作成
    list_1_rank_dict = dict((v,i) for i, v in enumerate(list_1))
    list_2_rank_dict = dict((v,i) for i, v in enumerate(list_2))
    # アイテム総数
    n = len(list_1)
    # 分散の総和
    var_sum = np.sum([(list_1_rank_dict[item] - list_2_rank_dict[item])**2 for item in list_1])
    
    return 1 - 6 * var_sum / (n**3 - n)

ケンドールの順位相関係数

2つのリスト $R$ 、 $R’$ の組み合わせ( $ _nC_2 $ 通り)を考えて、正順の組み合わせなら+1、逆順の組み合わせなら-1としたときの全組み合わせにおける割合で定義されます。

ここで、正順とは、$R_i > R_j $ かつ $R’_i > R’_j $ または、$R_i < R_i $ かつ $R'_j < R'_j $ となることで、逆順とは正順以外のパターンになることです。

計算例

2つのランクがあるリストにおける相関係数を考えます。

リスト $R$ := <1,2,3>
リスト $R’$ := <1,3,2>

このとき $R$ 、 $R’$ の組み合わせ以下の3つとなります。

$R$ : (1,2), $R’$ : (1,3)
$R$ : (1,3), $R’$ : (1,2)
$R$ : (2,3), $R’$ : (3,2)

このとき、正順の組み合わせは1,2で、逆順の組み合わせは3となるので、$\tau = (2-1)/(3(3-1)/2) = 0.333 $ となります。

定義

$$
\tau = \frac{G – H}{n(n-1)/2}
$$

$G$ ：正順となる組み合わせ総数
$H$ ：逆順となる組み合わせ総数

実装例

Pythonでの実装例は以下になります。

def kendall_corr(list_1: list, list_2: list) -> float:
    """
    ケンドールの順位相関係数を算出するメソッド。

    Parameters
    -------
    list_1 : list
        ランクで昇順ソートされたアイテムのリスト。
    -------
    list_2 : list
        ランクで昇順ソートされたアイテムのリスト。

    Returns
    -------
    kendall_correlation : float
        ケンドールの順位相関係数
    
    """
    
    # リストのアイテムがkey、ランクがvalueのdict作成
    list_1_rank_dict = dict((v,i) for i, v in enumerate(list_1))
    list_2_rank_dict = dict((v,i) for i, v in enumerate(list_2))
    # 正順組み合わせ数
    G = 0
    # 逆順組み合わせ数
    H = 0
    # アイテム総数
    n = len(list_1)
    # リスト内の全ての組み合わせについて
    for i, j in itertools.combinations(list_1, 2):
        # 正順ならGに1加算、それ以外ならHに1加算
        concordant_f = (
            ((list_1_rank_dict[i] > list_1_rank_dict[j]) & (list_2_rank_dict[i] > list_2_rank_dict[j]))
            | ((list_1_rank_dict[i] < list_1_rank_dict[j]) & (list_2_rank_dict[i] < list_2_rank_dict[j])))
        if concordant_f:
            G += 1
        else:
            H += 1
    
    return (G - H)/(n*(n-1)/2)

数学的解釈

ケンドールの順位相関係数は、その定義から確率論的な解釈が可能です。
以下の実験を考えます。

リスト $R$ からランダムにアイテムの組み合わせ $ (i,j) $ を1つ選ぶ
リスト $R'$ における1で選んだ組み合わせ $ (i,j) $ について、1と同じ大小関係なら1、それ以外なら0とする

上記の実験結果が1になる確率を数学的に定義すると以下となります。
$$
p = \frac{G}{_nC_2} = \frac{G}{n(n-1)/2}
$$
ここで、$p \in [0,1]$ なので、ケンドールの順位相関係数 $ \tau \in [-1,1]$ に揃えるため、以下の変換を行います。
\begin{eqnarray}
\tau &=& p-(1-p) = 2p -1 \\
&=& \frac{2G}{n(n-1)/2} - 1 \\
&=& \frac{2G - n(n-1)/2}{n(n-1)/2} \\
&=& \frac{G + G - n(n-1)/2}{n(n-1)/2} \\
&=& \frac{G - (n(n-1)/2 - G)}{n(n-1)/2} \\
&=& \frac{G - H}{n(n-1)/2}
\end{eqnarray}

以上より、ケンドールの順位相関係数を確率論的に解釈できることがわかりました。

AP correlation

$AP(Average\,Precision)$ をベースにすることで、リストにおける上位のランクでの誤りに対して大きなペナルティを与えられる指標です。
※$AP(Average\,Precision)$ の説明は以下がわかりやすいです。

mathwords.net

MAP（Mean Average Precision）という指標の意味 - 具体例で学ぶ数学

https://mathwords.net/meanap

MAP（Mean Average Precision、mAP）とは、推薦システム、検索システム、物体検出アルゴリズムなどの性能を表す評価指標です。APおよびMAPの意味と計算方法について解説します。

定義

$$ \tau_{ap}(list, actual) = \frac{2}{n - 1} \cdot \sum^n_{i=2}\left( \frac{C(i)}{i-1} \right) - 1 $$

$n$ ：リストの長さ
$C(i)$ ：ランク $i$ のアイテムと、ランク $i$ よりも上位のランクのアイテムとの組み合わせのうち、正順となる組み合わせの数

実装例

Pythonでの実装例は以下になります。

def ap_corr(rank_list: list, actual: list) -> float:
    """
    AP correlationを算出するメソッド。

    Parameters
    -------
    rank_list : list
        ランクで昇順ソートされたアイテムのリスト。
    -------
    actual : list
        ランクで昇順ソートされたアイテムのリスト（正解）。

    Returns
    -------
    AP correlation : float
        AP correlation
    
    """
    
    # リストのアイテムがkey、ランクがvalueのdict作成
    rank_dict = dict((v,i) for i, v in enumerate(rank_list))
    actual_rank_dict = dict((v,i) for i, v in enumerate(actual))
    # アイテム総数
    n = len(rank_list)
    
    sum_C = 0
    # ランク最上位のアイテムを除いてループ処理
    for index in range(n-1):
        # 比較対象のindex
        target_index = index + 1
        target = list_1[target_index]
        C = 0
        # 比較対象アイテムと、比較対象アイテムより上位のランクのアイテムとの組み合わせについて
        for i in list_1[:target_index]:
            # 正順ならCに1加算
            concordant_f = (
                ((rank_dict[target] > rank_dict[i]) & (actual_rank_dict[target] > actual_rank_dict[i]))
                | ((rank_dict[target] < rank_dict[i]) & (actual_rank_dict[target] < actual_rank_dict[i]))
            )
            if concordant_f:
                C += 1
        sum_C += C/(target_index)
    
    return sum_C/(n-1)

ここで、 $AP\,correlation$ は本質的には1つのランクがあるリストと正解データとを比較する指標なので、他の順位相関係数のように引数を入れ替えた場合の対称性はありません。
一方、正解データを考慮しない、純粋な2つのランクがあるリストに関して相関係数を算出する場合は、以下のように変換して対称性を獲得する必要があります。

$$
\tau_{synmetric \, ap}(list1, list2) = \frac{\tau_{ap}(list1, list2) + \tau_{ap}(list2, list1)}{2}
$$

def symmetric_ap_corr(list_1: list, list_2: list) -> float:
    """
    synmetric AP correlationを算出するメソッド。

    Parameters
    -------
    list_1 : list
        ランクで昇順ソートされたアイテムのリスト。
    -------
    list_2 : list
        ランクで昇順ソートされたアイテムのリスト。

    Returns
    -------
    synmetric AP correlation : float
        synmetric AP correlation
    
    """
    return (ap_corr(list_1, list_2) + ap_corr(list_2, list_1)) / 2

数学的解釈

$AP\,correlation$ は、ケンドールの順位相関係数と同様にその定義から確率論的な解釈が可能です。
以下の実験を考えます。

リスト $R$ から最上位のランク以外のアイテム( $i$ 位)をランダムに1つ選ぶ
1で選んだアイテムより上位のアイテム( $j$ 位)を1つ選ぶ
リスト $R'$ において同じ順番なら1、それ以外なら0とする

上記の実験結果が1になる確率を数学的に定義すると以下となります。
$$ p = \frac{1}{n-1} \cdot \sum^n_{i=2}\left( \frac{C(i)}{i-1} \right) $$
ここで、$p \in [0,1]$ なので、ケンドールの順位相関係数と同様に $ \tau_{ap} \in [-1,1]$ に揃えるため、以下の変換を行います。
$$ p-(1-p) = 2p -1 = \frac{2}{n - 1} \cdot \sum^n_{i=2}\left( \frac{C(i)}{i-1} \right) - 1 $$

以上より、ケンドールの順位相関係数と同様に $AP\,correlation$ を確率論的に解釈できることがわかりました。

指標比較

上記で定義したスピアマンの順位相関係数、ケンドールの順位相関係数、AP correlationの実装例をもとに、実際に2つのランクがあるリストの相関を比較します。
ここでは、東京大学出版統計学入門 (基礎統計学Ⅰ)p55に記載されている例を使用します。

import numpy as np
import itertools
import matplotlib.pyplot as plt

# テストデータ（東京大学出版 統計学入門 (基礎統計学Ⅰ)p55）
list_1 = ['桜', '菊', 'バラ', '梅', 'ゆり', 'チューリップ', 'カーネーション', '椿']
list_2 = ['菊', 'バラ', '桜', 'ゆり', '梅', 'カーネーション', 'チューリップ', '椿']

plt.figure(figsize=(20,10))
plt.bar(
    ['Spearman', 'Kendall', 'Symmetric AP'],
    [
        spearman_corr(list_1, list_2),
        kendall_corr(list_1, list_2),
        symmetric_ap_corr(list_1, list_2)
    ]
)
plt.title('Correlation coefficient comparison')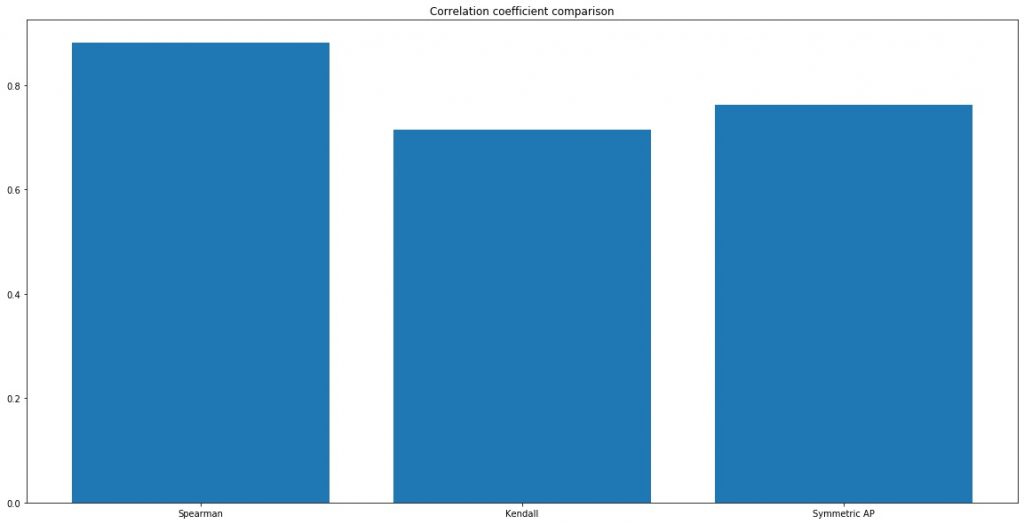

まとめ

$AP(Average Precision)$ はオフラインレコメンド指標の $MAP@K$ の計算過程ででてくるため知っていましたが、このように変形することで順位相関係数として活用できるというのは新鮮でした。
また、相関係数が確率論的に定義されることで解釈性をあげられるということも新しい発見でした。

参考

論文の他に、以下の書籍を参考にしました。

前の記事

『トークンエコノミービジネスの教科書』を読んだ感想 2020.04.11
次の記事

『効果検証入門〜正しい比較のための因果推論/計量経済学の基礎』を読んだ感想 2020.04.30

ランクがある2つのリストの相関係数の算出にAverage Precisionを導入する方法

スピアマンの順位相関係数

定義

実装例

ケンドールの順位相関係数

計算例

定義

実装例

数学的解釈

AP correlation

定義

実装例

数学的解釈

指標比較

まとめ

参考

『トークンエコノミービジネスの教科書』を読んだ感想 2020.04.11

『効果検証入門〜正しい比較のための因果推論/計量経済学の基礎』を読んだ感想 2020.04.30