MPR(Mean Percentage Ranking)〜暗黙的にユーザの嗜好を得られるレコメンドシステムにおけるオフライン評価指標の紹介
- 2020.04.08
- レコメンド
レコメンドシステムにおけるオフライン評価指標の一つであるMPR(Mean Percentage Ranking)について書かれた論文を見つけました。
今回はその調べた結果をまとめます。
ちなみに、レコメンド文脈でのオフラインorオンライン評価とは以下を意味します。
| 分類 | 説明 |
|---|---|
| オンライン評価 | 実際にユーザにレコメンドを実施し、ユーザがどれだけ反応したかを評価すること。 Ex. A/Bテスト |
| オフライン評価 | 仮想的にユーザにレコメンドを実施し、ユーザの行動をどれだけ予測できたかを評価すること。 Ex. MAP@K、Precision@K、Recall@K |
MPR(Mean Percentage Ranking)とは
MPR(Mean Percentage Ranking)はレコメンドされたアイテムに対するユーザの反応が暗黙的に得られる場合に使われる、Recall-orientedな指標です。
ここで、「暗黙的」にユーザの反応を得られるというのは、ユーザがレコメンドされたアイテムに対してどれだけクリックor閲覧したのか、またはどれだけ滞在したのかなど、ユーザが間接的にレコメンド結果を評価したとみなせるデータを取得できることを指します。
逆に「明示的」にユーザの反応を得られるというのは、レコメンドされたアイテムに対してGood、Badというようにユーザが直接的にレコメンド結果を評価したデータを取得できることを指します。
暗黙的にデータを取得する場合はPrecisionベースの指標は不適切
以下の論文によれば、レコメンドに対するユーザの反応を明示的に追跡できない場合(暗黙的にしか得られない)はPrecisionベースの測定指標は不適切とのことです。
Precisionベースの測定指標はユーザにとってどれくらいレコメンド結果が望ましくないかを図る指標です。
確かに、レコメンドしたアイテムがユーザにとって望ましいかったのか、そうでなかったのかはAmazonで商品を評価するために☆をつけたり、Youtubeでgoodボタンやbadボタンを押したりといった、レコメンド結果に対する明示的な評価がないとわかりません。
MPRの定義
MPRの定義は以下になります。
$$ MPR = \frac{\sum_{u \in U}\sum_{i \in l(u)} r_{u,i} \overline{rank_{u,i}}}{\sum_{u \in U}\sum_{i \in w(u)} r_{u,i}} $$
- \( U \) はユーザの集合
- \( l(u) \) はユーザ \( u \) へのレコメンドしたアイテムの集合
- \( r_{u,i} \) はユーザ \( u \) がレコメンドされたアイテム \( i \) に反応した場合は1、それ以外は0
- \( \overline{rank_{u,i}} \) はユーザ \( u \) がレコメンドされたアイテム \( i \) におけるリスト内のランクをパーセントに変換した数値。
例えば、リストで最上位(通常は類似度が最大)のアイテムの場合は0%、リストで最下位の(通常は類似度が最小)のアイテムの場合は100%になります。
MPRは順位付けされたレコメンド結果に対するユーザの満足度を測定し、低いほど望ましい指標となります。
実装
MPRの定義をもとに実装してみました。
ここではMPRを他の指標と比較するために、Recallも実装しています。
※通常、Recall@Kのようにレコメンド結果の上位いくつを計測するかも考慮しますが、今回は簡潔な実装のため@Kを実装していません。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
def mean_percentage_ranking(preds: list, actuals: list):
"""
MPRを算出する。
Parameters
----------
preds : list
レコメンドアイテムの2次元list。
actuals : list
ユーザが嗜好したアイテムの2次元list。
Returns
----------
mpr : float
mpr
Examples
--------
>>> preds = [[1,2,3],[4,5,6]]
>>> actuals = [[1,2,5,6],[3,4,5]]
>>> mean_percentage_ranking(preds, actuals)
"""
def sum_percentage_ranking(pred, actual):
actual_set = set(actual)
pred_set = set(pred)
return sum([pred.index(i)/len(pred)*100 for i in actual_set if i in pred_set])
sum_list = [sum_percentage_ranking(pred, actual) for pred, actual in zip(preds, actuals)]
return sum(sum_list)/len(sum_list)
def recall(pred, actual):
"""
Recallを算出する。
Parameters
----------
pred : list
レコメンドアイテムのlist。
actual : list
ユーザが嗜好したアイテムのlist。
Returns
----------
mpr : float
mpr
Examples
--------
>>> preds = [1,2,3]
>>> actuals = [1,2,5,6]
>>> recall(preds, actuals)
"""
actual_set = set(actual)
pred_set = set(pred)
return len(actual_set & pred_set)/len(actual_set)サンプルデータをもとにMPRとRecallを比較します。
# サンプルデータ作成
preds = [[1,2,3],[4,5,6]]
actuals = [[1,2,5,6],[3,4,5]]
# MPR算出
mpr_score = mean_percentage_ranking(preds, actuals)
# Recallを算出(MPRと比較するため%に変換)
recall_score = np.mean([recall(pred, actual) for pred, actual in zip(preds, actuals)])*100
plt.figure(figsize=(20,10))
plt.bar(['MPR', 'Recall'], [mpr_score, recall_score], color=['#e41a1c', '#377eb8'])
plt.ylim(0,100)
plt.ylabel('percentage')
plt.title('MPR and Recall')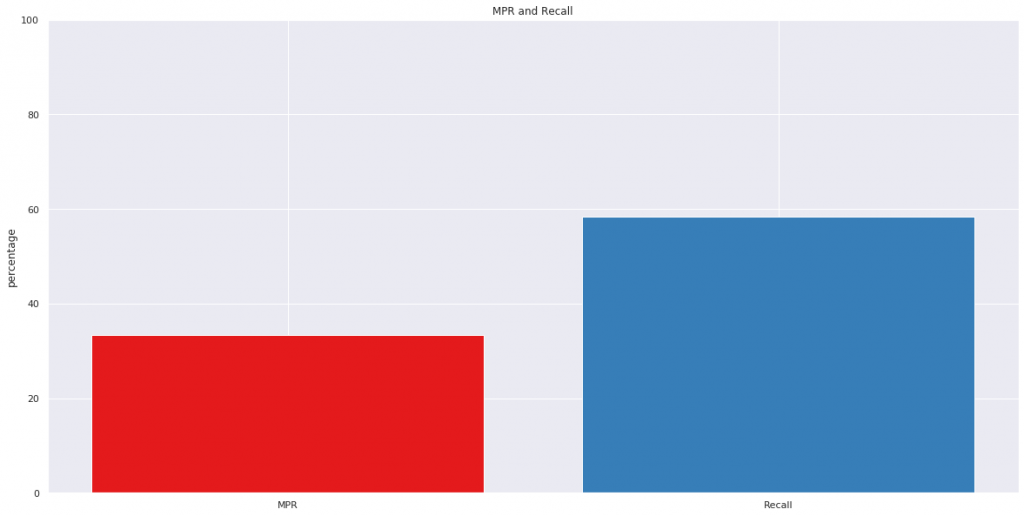
サンプルデータを少し変えて、MPRとRecallを比較します。
# サンプルデータ作成
preds = [[1,2,3],[4,5,6]]
actuals = [[5,6],[3,6]]
# MPR算出
mpr_score = mean_percentage_ranking(preds, actuals)
# Recallを算出(MPRと比較するため%に変換)
recall_score = np.mean([recall(pred, actual) for pred, actual in zip(preds, actuals)])*100
plt.figure(figsize=(20,10))
plt.bar(['MPR', 'Recall'], [mpr_score, recall_score], color=['#e41a1c', '#377eb8'])
plt.ylim(0,100)
plt.ylabel('percentage')
plt.title('MPR and Recall')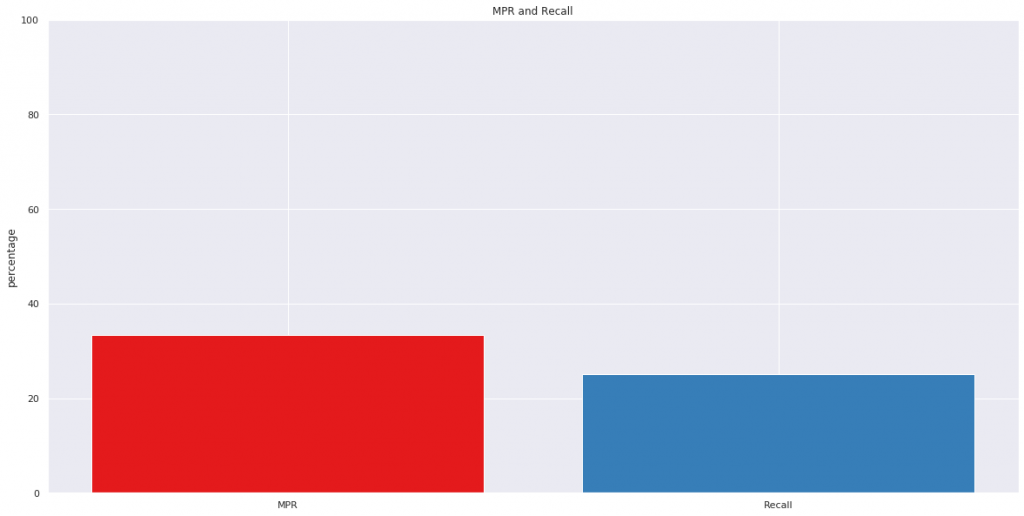
MPRは同じであるものの、Recallが低い結果となりました。
考察
MPRは定義上、ユーザが嗜好したアイテムを1件もレコメンドしていない場合は0になりますが、ユーザが嗜好したアイテムがレコメンドリストの最上位の場合もMPRは0となります。
MPRに加えてRecallも測定したり、ユーザが嗜好したアイテムが1件も含まれていない場合は何らかの罰則をMPRに加えるなどの工夫をすることで、より使いやすい指標になりそうです。
- 前の記事

『外資系コンサル流・「残業だらけ職場」の劇的改善術 「個人の働き方」も「組織の体質」も変わる7つのポイント』を読んだ感想 2020.02.16
- 次の記事

『トークンエコノミービジネスの教科書』を読んだ感想 2020.04.11