プロ野球の規定打席数は「大数の法則」で裏付けできる？

手始めに、統計理論の投稿をしてみます。

今回のテーマは、統計理論でも超有名な「大数の法則」です。

今夜CSの中継もありましたし、プロ野球の規定打席数との関係を説明します。

まずは、大数の法則をざっくりと説明し、そのあとで、プロ野球の規定打席数の定め方が、「大数の法則」に則っていることをシミュレーションにより確かめます。

大数の法則とは

一言でいえば、次の通りです。

例として、コイン投げを考えてみましょう。
表が出ることを成功、裏が出ることを失敗とします。
ちなみに、このコインをまったく歪みがない新品と仮定すると、成功率は0.5になるはずです。
これを真の成功率と呼ぶことにします。
さて、コインを投げてみましょう。
2、3回だけのコイン投げであれば、全部が成功、全部が失敗だなんてことがあるかもしれません。
ですが、10回、20回とコイン投げの回数を増やしていくと、成功率が0.5に近づいていく気がしませんか？
これが大数の法則と呼ばれる、感覚的にも理解しやすい確率法則なのです。

余談ですが、世の中には「大数の法則」を理解できていない、しようとしない経営者がいます。
データ利活用が発展していく今後のビジネスの世界で、こういった統計リテラシーを貪欲に学ぼうとしないのは末恐ろしいことです。

（注意）ここでは数式を使った厳密な説明を避け、簡易にまとめています。

プロ野球の規定打席数と「大数の法則」

規定打席数の定義

プロ野球には規定打席数なるものが存在します。
以下、wikipediaからの引用です。

規定打席（きていだせき）とは、プロ野球において、リーグが発表する打撃ランキングの対象となるために必要な打席の数のことである。

現在の規定打席数は以下の式で計算できます。（※）

・所属球団の試合数 × 3.1

各球団の試合数は143ですから、規定打席数は 143 × 3.1 = 443 ですね。
しかし、この規定打席数ってどんな根拠があって定められているんでしょうか？
規定打席数を決めている基準が気になるところ…。

さて、ここで「大数の法則」が登場です。

※『野球規則10・22(a)』より

「大数の法則」による規定打席数の裏付け

では、実際にシミュレーションを用いて規定打席数の設定が妥当かどうかを検証してみましょう。
ここでは、真の打率が 0.3 の選手が存在したとして、1,000 打席バッターボックスに立ったとしましょう。（※）
「真の打率」という言葉を不自然に感じるかもしれませんが、コインの表が1/2で出る、サイコロの1の目が1/6で出るというのと同じ話です。
「理想的な打率」と同義かもしれません。
また、1,000打席というのも極端な話ですが、シミュレーションなので割り切ってください（笑）

さて、打席数の増加により、ある選手の打率が、真の打率へ近づいていく様子を見てみましょう。

統計解析言語Rを使ってグラフを出力しています。
以下がサンプルコードです。

unif_sample <- runif(n=1000, min=0, max=1)
hit_rate <- numeric(1000)
cnt <- 0
for(i in 1:1000){
	if(unif_sample[i]<=0.3){
		cnt <- cnt+1
	}
	hit_rate[i] <- cnt/i
}
plot(hit_rate, ylim=c(0,0.5), ylab="hit rate", xlab="number of trial", type="l")
abline(h=0.3, v=443)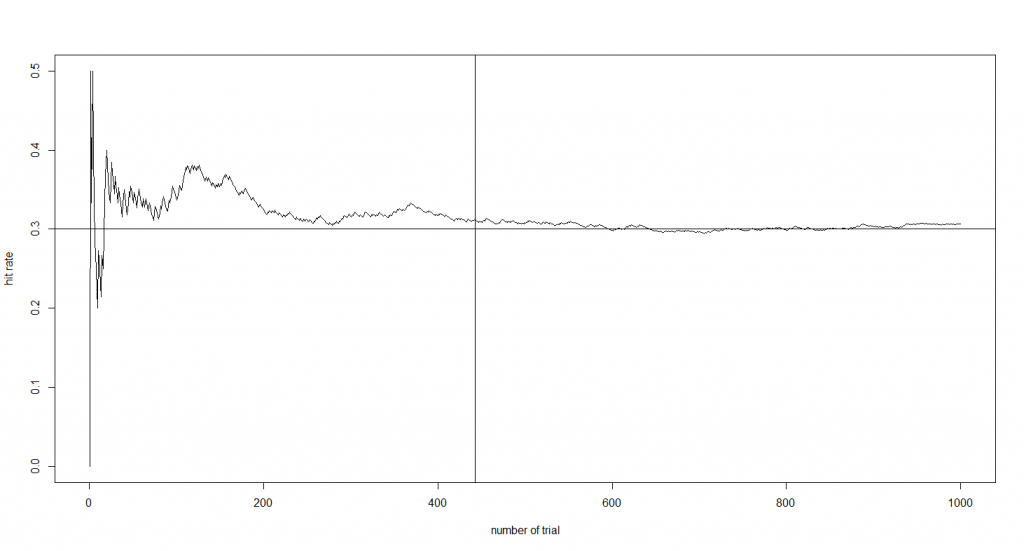

縦軸は打率、横軸は打席数、グラフ中の縦線は規定打席数、横線は真の打率です。
グラフを見ると、規定打席数付近で、真の打率へかなり集中していることがわかります。
NPBが規定打席数を定める際に「大数の法則」を考慮していたかどうかはわかりませんが、シミュレーション結果からみると、規定打席数の定め方には説得力がありそうです。