ランダムフォレストで近接グラフを可視化する方法
前回に引き続き決定木系のお話になりますが、今回は近接グラフ(proximity plot)を可視化する方法を紹介します。
近接グラフはランダムフォレスト(RandomForest)を構成する各決定木の終端ノードに属するデータに着目した、データ間の近さを可視化する手法です。
※前回は特徴量の解釈には重要度だけでなく部分依存グラフも活用しようという記事を書きました。
近接グラフとは
近接グラフとは、学習データ間の近さを意味する近接行列を多次元尺度構成法(Multi-Dimensional Scaling:MDS)によって可視化したグラフのことです。
以降では、近接グラフの可視化に必要な近接行列、多次元尺度構成法について説明します。
近接行列とは
近接行列は対象のデータ数を \(N\) とすると、行・列ともにデータのインデックスとする \(N \times N\) の行列になります。
例えば、近接行列の \(i\) 行 \( j \) 列の要素はデータ \(i\) とデータ \(j\) の近接度を意味します。
近接行列の要素は次の2ステップで算出できます。
- ランダムフォレストを構成する木について、終端ノードに共にデータが存在するならば該当する行列要素に1を加算、これを全ての木で繰り返す
- 最後に木の数で割る(行列要素の標準化)
近接行列算出のイメージは次の通りです。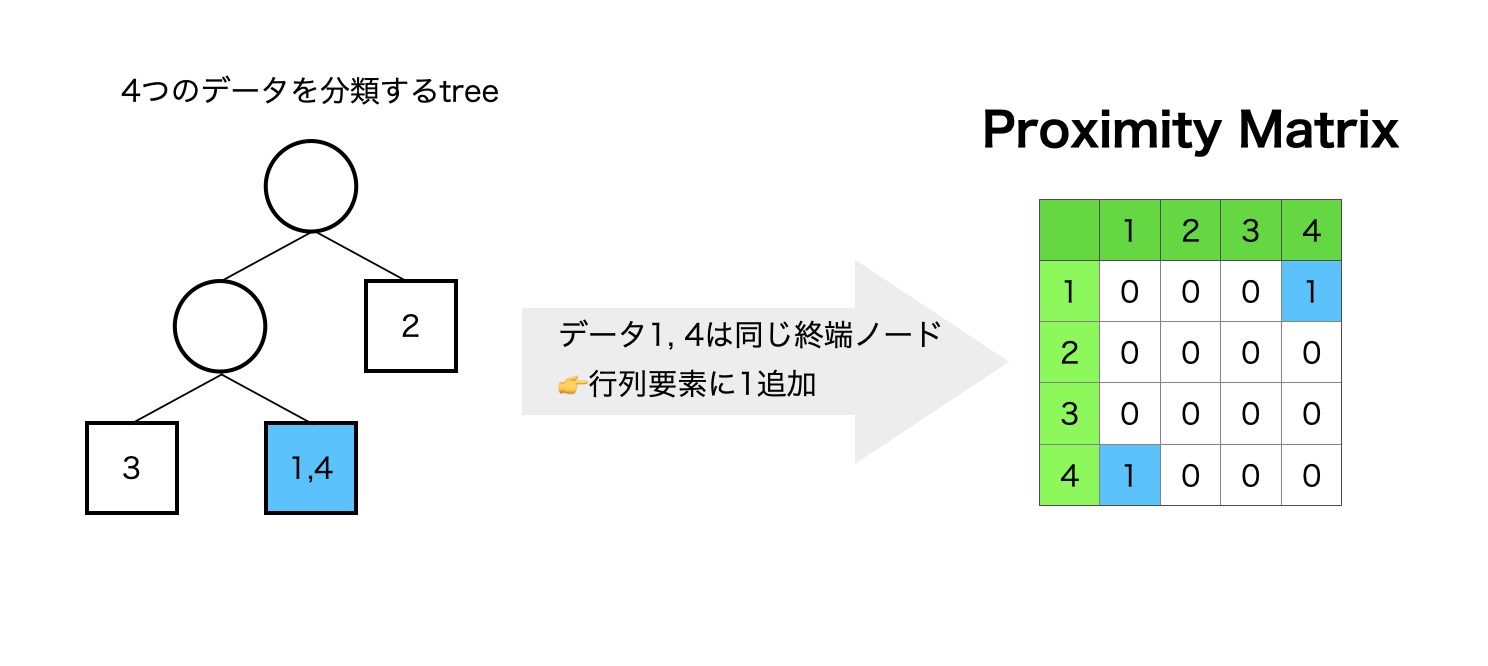
また、UC Berkeley(カルフォルニア大学バークレー校)の統計学コンテンツで近接行列(Proximities)の説明を見つけたのでこちらも引用しておきます。
These are one of the most useful tools in random forests. The proximities originally formed a NxN matrix. After a tree is grown, put all of the data, both training and oob, down the tree. If cases k and n are in the same terminal node increase their proximity by one. At the end, normalize the proximities by dividing by the number of trees.
出展: https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm#prox
多次元尺度構成法とは
距離行列や類似度行列といった多次元のデータを2次元や3次元などの低次元に写像し、視覚化する手法です。
これだけ聞くと多次元尺度構成法は主成分分析と近そうに思えますが、まったくコンセプトが異なります。
多次元尺度構成法と主成分分析の違いについては以下で詳しく記載されているので、興味があればご参照ください。
実装
近接グラフを実装するコードを紹介します。
なお、コードはGitHubにあげております。
動作環境やPythonライブラリに関しては以下のファイルを参照してください。
- Dockerfile
- pyproject.toml
- poetry.lock
データの読み込みとモデル構築
scikit-learnのirisデータセットを読み込み、ランダムフォレストで学習します。
今回は近接グラフを可視化することが目的なので、ハイパーパラメータはデフォルトのままにしています。
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.manifold import MDS
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
sns.set()
# irisデータセットをロード
data = load_iris()
train_X = data['data']
train_y = data['target']
features = data['feature_names']
target_names = data['target_names']
rfc = RandomForestClassifier()
rfc.fit(train_X, train_y)近接行列の算出
次に近接行列を算出します。
近接行列を算出するライブラリはPythonで実装されていないようなので、定義をもとにスクラッチで実装します。
なお、以下のコードはこちらを参考に実装しています。
def proximityMatrix(model, X, normalize=True):
"""
近接行列を算出する
Notes:
https://stackoverflow.com/questions/18703136/proximity-matrix-in-sklearn-ensemble-randomforestclassifier
"""
terminals = model.apply(X)
data_size, nTrees = terminals.shape
proxMat = np.zeros([data_size, data_size])
for i in range(nTrees):
belong_node = terminals[:, i]
proxMat += 1*np.equal.outer(belong_node, belong_node )
if normalize:
proxMat = proxMat / nTrees
return proxMat
proximity_matrix = proximityMatrix(rfc, train_X, normalize=True)
print(f'proximity_matrix.shape: {proximity_matrix.shape}')OUTPUT:
proximity_matrix.shape: (150, 150)
データ数が150なので、近接行列のサイズは150×150になります。
近接行列のままでは次元数が多すぎて可視化に相応しくないので、多次元尺度構成法によって150次元から2次元空間に写像して、可視化できるデータに変換する必要があります。
近接グラフの可視化
多次元尺度構成法はPythonのsklearn.manifold.MDSで実装されています。
mds = MDS(n_components=2, random_state=0)
proximity_matrix_mds = mds.fit_transform(proximity_matrix)
print(f'proximity_matrix_mds.shape: {proximity_matrix_mds.shape}')OUTPUT:
proximity_matrix_mds.shape: (150, 2)
データを150次元から2次元に削減できたので、これで可視化できるようになりました。
ターゲット変数[0, 1, 2]にラベル名を割り当て、近接グラフを作図します。
# ラベルを追加
tmp = np.concatenate([pos, train_y[:, np.newaxis]], axis=1)
# DataFrame化
df_for_plot = pd.DataFrame(tmp, columns=['x1', 'x2', 'label'])
# ラベルを名称に変換
df_for_plot['label'] = df_for_plot['label'].map(lambda x: target_names[int(x)])
# 近接グラフの可視化
sns.scatterplot(x='x1', y='x2', data=df_for_plot, hue='label')
plt.title('proximity plot')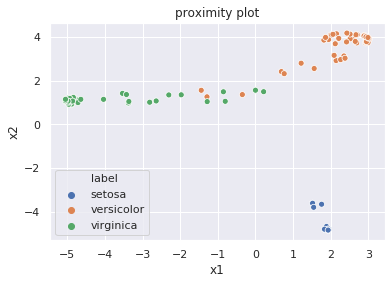
近接グラフを確認したところ、視覚的にラベルごとにグルーピングできそうなので、ランダムフォレストによる分類がうまくいっていると言えます。
ここで、顕著にグルーピングできるデータ郡(右下のsetosaや右上のversicolor)は、ランダムフォレストを構成する多くの木で同じ終端ノードに所属しているデータになります。
これらのデータはどの木でも似ているデータだと判断した結果なので、分類確度がより高いデータと言うこともできるでしょう。
参考
- 前の記事
特徴量重要度だけで解釈するのはやめよう~部分依存グラフのすすめ 2021.02.12
- 次の記事
TableauのLOD表現をSQLで理解する 2021.02.15