特徴量重要度だけで解釈するのはやめよう～部分依存グラフのすすめ

2021.02.12
機械学習
決定木

以前、決定木アルゴリズムの特徴量重要度(feature_importance)に関する記事を書きましたが、依然としてターゲット変数に寄与する特徴量を重要度だけで解釈するケースを良く見かけます。

https://yolo-kiyoshi.com/2019/09/16/post-1226

機械学習案件で、どの特徴量がターゲットの分類で「重要」かを知るためにRandamForestやXGBoostなどの決定木系アルゴリズムの重要度(importance)を確認するということがよくあります。ただ、この重要度がどのように計算されているのかを知らずに、なんとなく「重要」な特徴量をあぶり出してくれる便利なツールとして使われていまっているような印象があります。確かに重要度はお手頃に求められる指標でいかにも特徴量の「重要」度を良く説明しているように見えますが、実際にどれくらいターゲットの分類で効いているのかを聞かれると答...

データサイエンティスト同士で分析結果を共有するならば問題ないかもしれませんが、データサイエンティスト以外の方に特徴量重要度をもとにした分析結果を報告する際はあらぬ誤解を招く可能性があります。
※データサイエンティスト自身が特徴量重要度とは何かを把握せずに使っているケースもちらほらあります。
特徴量重要度が大きいということは、その変数を使ってノードを分割すると不純度が大きく減少するという意味しかありません。
重回帰モデルにおける偏回帰係数のように、その特徴量がターゲット変数に与える効果(その特徴量が1単位変化したときにどれだけターゲット変数に影響を及ぼすか)を意味しているわけではないのです。

また、「その変数の重要度が大きいのは分かったが、じゃあCVR(ターゲット変数)を増やすには具体的にどうすればいいのか？」と質問されると、特徴量重要度しか把握できていない場合は答えに窮すること間違いなしです。

今回は特徴量重要度だけでは解釈できないターゲット変数との定量的な関係性を、部分依存グラフ(Partial Dependece Plot: PDP)を活用して可視化する方法を紹介します。
部分依存グラフをうまく利用することで、「この変数をxxだけ増加させるとそれに比例してCVR(ターゲット変数)が増加するので、yyまで段階的に引き上げてみましょう」といった提案ができるようになります。

1. 部分依存グラフとは
- 1.1. 数式での定義
2. 実装
- 2.1. 数式の定義から実装
- 2.2. scikit-learnでの実装
3. 最後に
4. 参考

部分依存グラフとは

機械学習の入門書として有名な『はじめてのパターン認識』では、部分依存グラフを以下と定義しています。

ある特徴の値がクラスの識別にどのように寄与しているのかを、ほかの特徴量の寄与を加味したうえで見る指標 (p195)

つまり、重回帰モデルでの効果検証と同様に、他の特徴量の効果を固定したうえで興味がある特徴量とターゲット変数の関係性を記述できるということです。

数式での定義

特徴量 $X$ を $m$ 個の特徴ベクトル$x_1,\, \cdots,\, x_m$で構成される行列とします。
部分依存グラフを算出したい特徴ベクトルを $x_t$ ($ 1 \leq t \leq m $)とし、この $x_t$ の要素すべてをある値 $s$ に置き換えた特徴量を $X^{(t:s)}$ とします。
このとき、クラス $k$ の置換された $s$ に対する部分依存グラフ $ f_k(X^{(t:s)}) $ を以下で定義します。

$$ f_k \left(X^{(t:s)}\right) = \sum_{i=1}^{N}\left(\log p_k \left(X_i^{(t:s)}\right) – \frac{1}{K}\sum^{K}_{j=1}\log p_j \left(X_i^{(t:s)}\right) \right) $$

ここで、数式に含まれる記号は以下を意味しています。

$p_k(\cdot)$: クラス $k$ に分類される確率
$K$ :クラス数
$X_i^{(t:s)}$ : $x_t$ の要素すべてをある値 $s$ に置き換えた特徴量 $X^{(t:s)}$ の $i$ 番目のデータ
$N$: 学習データ数

なお、上記は『初めてのパターン認識』p196の定義です。

RのPartial Dependence Plotの公式ドキュメントを見ると、定義は以下となっています。
$$ f_k \left(X^{(t:s)}\right) = \frac{1}{N}\sum^{N}_{i=1} p_k \left(X_i^{(t:s)}\right) $$
scikit-learnの公式ドキュメントでも同様の定義となっていたので、こちらの方が正しいのかもしれません。

実装

scikit-learnのirisデータセットで部分依存グラフを算出し、可視化します。
なお、今回は話を単純化するためにターゲット変数のsetosa, virginicaを同じクラスに変換し、多クラス分類問題ではなく２値分類問題としています。
※『はじめてのパターン認識』でも同様の処理をしています。
まず、データを読み込んでRandomForestで学習し、特徴量重要度を可視化してみます。

ちなみに、今回紹介するコードはGitHubにあげております。
動作環境やPythonライブラリに関しては以下のファイルを参照してください。

Dockerfile
pyproject.toml
poetry.lock

INPUT:

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier

from matplotlib import pyplot as plt

import numpy as np

import pandas as pd

import seaborn as sns
sns.set()

# irisデータセットをロード
data = load_iris()

train_X = data['data']
train_y = data['target']
features = data['feature_names']
target_names = data['target_names']

# setosa, virginicaを同じラベルに変更
train_y = np.where((train_y == 0) | (train_y == 2), 0, 1)

rfc = RandomForestClassifier()

# 特徴量重要度を可視化
rfc.fit(train_X, train_y)
plt.barh(features, rfc.feature_importances_)
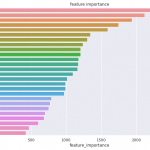
plt.title('feature importances')

OUTPUT: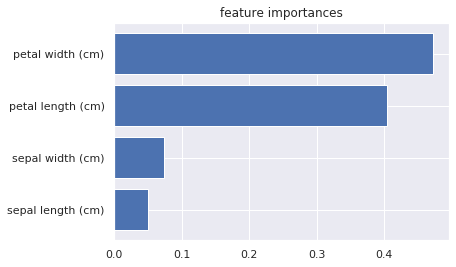

この分類タスクでは、「Petal Width(cm)」の重要度が最も大きいことがわかりますが、「Petal Width(cm)」がどの程度クラス分類に寄与するのかはわかりません。
この分類タスクでは「Petal Width(cm)」が重要なんだなぁ、くらいしか情報を得られないのです。

こんなとき、部分依存グラフを算出することでより深く特徴量を解釈することができます。
部分依存グラフの可視化によって、「Petal Width(cm)」とクラス分類との関係性を定量的に把握できるからです。

数式の定義から実装

以降、「数式での定義」に沿ってコーディングし、部分依存グラフを算出、可視化します。

def pdp(model, df, feature, target=1):
    """
    Partial dependence plots(部分依存グラフ)を作図する
    """
    df_ = df.copy()
    x = list()
    y = list()
    # 対象の特徴量の最小値から最大値までに0.1刻みのシーケンスを作成
    seq_list = np.arange(np.min(df[feature]), np.max(df[feature]), 0.1)
    
    for seq in seq_list:
        # 対象の特徴量の値を書き換える
        df_.loc[:, feature] = seq        
        # クラス所属確率が0の場合にエラーになるためlog1pを使用
        pred_list = np.log1p(model.predict_proba(df_))
        
        sum_pred_prob = 0
        for pred in pred_list:
            # クラス所属確率の対数の和
            sum_log_prob = np.sum([pred[k] for k in range(len(pred))])/len(pred)
            sum_pred_prob += (pred[target] - sum_log_prob)
        
        x.append(seq)
        y.append(sum_pred_prob)
    
    plt.plot(x, y)
    plt.xlabel(feature)
    plt.ylabel('partial dependence')
    plt.title('Partial dependence plots')

df_train = pd.DataFrame(train_X, columns=features)
pdp(rfc, df_train, 'petal width (cm)', target=1)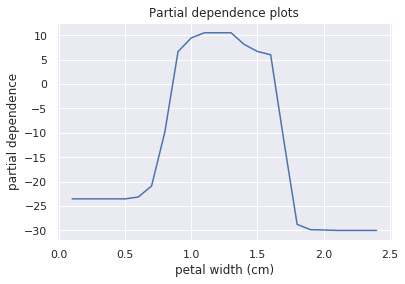

横軸は「Petal Width(cm)」で、縦軸はクラス分類に対する寄与度(部分依存性)になります。
「Petal Width(cm)」が0.65~0.9でクラス分類に対する寄与度は線形的に増加するものの、0.9~1.6まではほぼ横ばい、1.6以降は減少しています。
このように部分依存グラフによって特徴量重要度では確認できなかった、特徴量とターゲット変数との定量的な関係性を把握できることが分かりました。

scikit-learnでの実装

scikit-learnには部分依存グラフを可視化するためのplot_partial_dependenceというライブラリが存在します。
このライブラリでは、1つの特徴量における部分依存グラフだけではなく、2つの特徴量の相互作用の部分依存グラフも可視化できます。
なお、部分依存グラフの算出方法に関しては今回紹介している『はじめてのパターン認識』の定義と異なるので注意してください。
※定義は公式ドキュメントを参照してください

# from scikit-learn
# https://scikit-learn.org/stable/modules/partial_dependence.html
from sklearn.inspection import plot_partial_dependence

fig = plt.figure(figsize=(20, 7))
ax = fig.add_subplot(1, 1, 1)
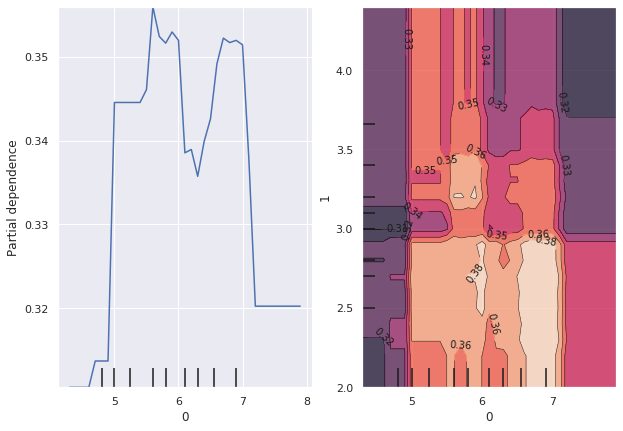
plot_partial_dependence(rfc, train_X, (3, 2, [3, 2]), target=1, ax=ax)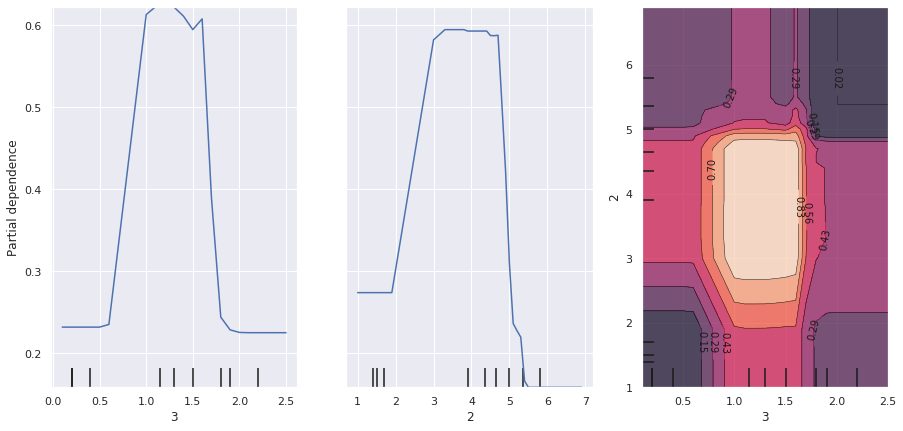

左から2つの図は4列目(Petal Width(cm))、3列目(Petal Length(cm))の特徴量の部分依存グラフです。
一番右の図は4列目、3列目の相互作用の部分依存グラフで、等高線が高いほど部分依存性が大きいことを意味しています。2変数正規分布をイメージするとわかりやすかもしれません。

最後に

決定木系のアルゴリズムは重回帰モデルに比べると特徴量の標準化などが必要がないためにお手軽に使えて、パラメータチューニングしなくてもそこそこの精度が出て、その上、特徴量重要度という一見わかりやすい指標も出力してくれるので、分析の初手では重宝されます。
しかし、単純に予測精度を追求するだけならいざ知らず、分析用途で利用する場合は注意が必要です。
最低限自分が使う手法の特色くらいは理解しておくべきだなと改めて思います。

参考

前の記事

LGBMRankerを使ってAmazonのレビューデータセットでランク学習してみる 2021.02.08
次の記事

ランダムフォレストで近接グラフを可視化する方法 2021.02.13