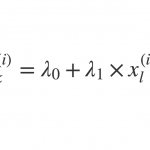肺ガンデータセットに一般化線形モデルや一般化線形混合モデルを適用してみる

2021.01.16
統計解析

あけましておめでとうございます。新年１発目の投稿です。

今後の業務で一般化線形混合モデル(GLMM)や状態空間モデルを使うかもしれないということで、再び統計モデリングを勉強しています。

今まで担当してきた業務は自然言語処理やレコメンドなどの機械学習モデルを扱ったものばかりで、GLMMや状態空間モデルに関して実務で使うことはありませんでした。

今回は簡単ではありますがscikit-learnの肺ガンデータセットをもとに、GLMやGLMMによるモデリングをやってみます。

コードはGitHubにあげています。

1. 環境
2. データ読み込みと可視化
3. 多重共線性への対応
4. PyStanでモデリング
- 4.1. 一般化線形モデル(GLM)
- 4.2. 一般化線形混合モデル(GLMM)
5. 最後に
6. 参考

環境

本記事で紹介しているコードはDockerコンテナ上での動作を想定しています。
なお、Dockerコンテナではなくても以下のライブラリをインストール済みであれば動作するはずです。
※依存ライブラリについてはGitHubのpyproject.tomlやpoetry.lockを確認してください。

Python 3.7
pandas==’0.25.3′
numpy==’1.18.1′
sklearn==’0.22.1′
seaborn==’0.9.0′
matplotlib==’3.1.2′
statsmodels==’0.12.1′
pystan==’2.19.1.1′
arviz==’0.10.0′

データ読み込みと可視化

scikit-learnの肺ガンデータセットをロードし、目的変数と説明変数のboxplot(箱ヒゲ図)を作図します。

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()
from sklearn.datasets import load_breast_cancer

# 肺ガンデータセットのロード
data = load_breast_cancer()
# 出力結果: (569, 30)
print(data.data.shape)

# 目的変数と説明変数のboxplot
df_viz = pd.concat(
    [pd.DataFrame(data.target, columns=['is_benign']), pd.DataFrame(data.data, columns=data.feature_names)],
    axis=1
)
plt.figure(figsize=(20, 30))
for i, feature in enumerate(data.feature_names):
    plt.subplot(6, 5, i+1)
    sns.boxplot(x='is_benign', y=feature, data=df_viz)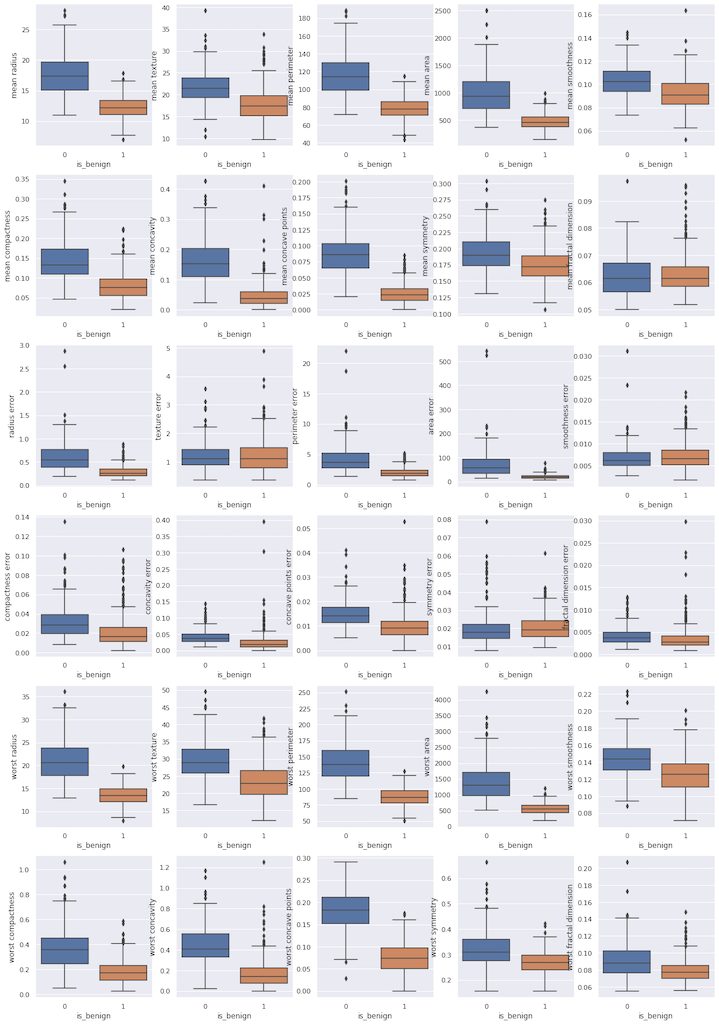

横軸は肺ガンの有無(1なら良性、0なら悪性)で、縦軸は各説明変数の値です。
目的変数である肺ガンの有無によって、四分位範囲が大きく異なる説明変数がいくつか存在することがわかります。

次に説明変数間の関係を確認します。
説明変数は全部で30個あるため、seabornライブラリのpairplot()でまとめて30×30の散布図を可視化するのは現実的ではありません。
なので、以下のように説明変数間の相関行列をもとに、高い相関係数の変数ペアが存在するかどうかを確認します。

import numpy as np

def get_high_corr_pairs(df, thred=0.8):
    """
    相関係数が閾値以上の変数の組み合わせを取得する
    """
    pairs = list()
    variables = list(df.columns)
    for num, row in enumerate(np.array(df.corr())):
        over_index = np.where(row[num + 1:] > thred)[0]
        if len(over_index) > 0:
            pairs.extend([(variables[num], variables[index + 1]) for index in over_index])
    return pairs

df_feature = pd.DataFrame(data.data, columns=data.feature_names)
# 出力結果: 44
print(len(get_high_corr_pairs(df_feature, thred=0.8)))

相関係数が0.8を超える説明変数のペアが44組存在することがわかりました。
このように説明変数間の相関係数が高くなる事象を多重共線性(マルチコ)といいます。
30個の説明変数全てを回帰モデルに入れると、多重共線性(マルチコ)によって推定したいパラメータの分布が不安定になります。
※多重共線性(マルチコ)については以前にブログで書きました。

キヨシの命題

統計学と機械学習におけるマルチコ（多重共線性）に対する考えの相違

https://yolo-kiyoshi.com/2019/05/27/post-1160

先日、デスマーチの末なんとか機械学習案件のリリースに漕ぎ着けました。今回の案件に関わらないですが、要件や仕様はしっかり明文化しておくべきですね。後から(特にリリース間近になって)言った言わないの議論になるのは双方にとってあまり気持ちのいいものではありません。些細な仕様変更のため口頭で合意した内容でも、しっかりと資料化しておくことの重要さを再認識しました。さて、今回はマルチコ（多重共線性）について投稿します。クライアント先で多変量解析をしているときにこの話題が出たので、いろいろと調べてみました。...

多重共線性への対応

多重共線性の原因となっている説明変数を取り除くことで、パラメータの推定値の分布が安定します。
今回は多重共線性を評価する指標の1つであるVIF値に応じて説明変数を一つずつ取り除いていきます。
ちなみにVIF値とは、ある説明変数を目的変数とし、それ以外の全ての説明変数で線形回帰を行った場合の決定係数 $R^2$ をもとに、$1/(1-R^2)$ で与えられます。

from statsmodels.stats.outliers_influence import variance_inflation_factor

def drop_col_by_vif(df, thred=10):
    """
    VIF値が閾値を超える変数を削除する
    """
    def get_max_vif(df):
        """
        VIF値が最大の変数とVIF値を取得する
        """
        vif = np.array([variance_inflation_factor(df.values, i) for i in range(df.shape[1])])
        variable = np.array(df.columns)[np.argmax(vif)]
        max_vif = np.max(vif)
        
        return variable, max_vif
    
    df_ = df.copy()
    # 閾値未満のVIF値が存在しなくなれば処理終了
    while True:
        variable, max_vif = get_max_vif(df_)
        if max_vif > thred:
            print(f'drop variable:{variable}, VIF:{max_vif}')
            df_.drop(columns=variable, inplace=True)
        else:
            break
    
    return df_

# VIF値が閾値を超える変数を削除する
df = drop_col_by_vif(df_feature, thred=10)

OUTPUT:

drop variable:mean radius, VIF:63306.17203588469
drop variable:worst radius, VIF:7573.943486033555
drop variable:mean perimeter, VIF:3901.901687119607
drop variable:worst perimeter, VIF:668.3854404127386
drop variable:mean fractal dimension, VIF:508.08682464149285
drop variable:worst smoothness, VIF:368.0533791867144
drop variable:worst texture, VIF:309.54444960438434
drop variable:worst fractal dimension, VIF:184.67972071700538
drop variable:worst symmetry, VIF:167.30971478504884
drop variable:mean concavity, VIF:142.29904340088856
drop variable:radius error, VIF:104.99215955661566
drop variable:worst concave points, VIF:100.94649021325061
drop variable:mean smoothness, VIF:86.99658368431041
drop variable:mean compactness, VIF:74.72314541276282
drop variable:mean area, VIF:67.47169344522399
drop variable:worst compactness, VIF:49.02308700997905
drop variable:perimeter error, VIF:43.72833047786977
drop variable:mean symmetry, VIF:36.0757931560618
drop variable:mean texture, VIF:23.709901129257826
drop variable:concave points error, VIF:18.16312090582923
drop variable:compactness error, VIF:15.728368747925318
drop variable:worst area, VIF:13.976625992787914
drop variable:mean concave points, VIF:11.176654130350768

23個の説明変数が削除され、以下の7個の説明変数だけが残りました。

print(f'selected variables:{list(df.columns)}')

selected variables:['texture error', 'area error', 'smoothness error', 'concavity error', 'symmetry error', 'fractal dimension error', 'worst concavity']

PyStanでモデリング

VIF値をもとに多重共線性を引き起こす説明変数を取り除いたので、いよいよモデリングをしていきます。
本記事では、MCMCサンプリングによるベイズ統計モデリングを実装できるPyStanを使用して、一般化線形モデル(GLM)や一般化線形混合モデル(GLMM)を構築します。
なお、Stanの使い方については以下の書籍が詳しいです。
PyStanではPythonからStanを呼んでいるだけなので、基本的にはStanの使い方がわかっていれば使いこなせるはずです。

一般化線形モデル(GLM)

まずは一般化線形モデル(GLM)でパラメータを推定します。
以下のようにdataブロックに入力するデザイン行列、目的変数、行列・ベクトルサイズを指定します。

# デザイン行列
X = df
X['intercept'] = 1
#目的変数
Y = data.target
# 行列・ベクトルサイズ
N, K = df.shape

また、一般化線形モデルで指定する線形予測子、リンク関数、確率分布はそれぞれ以下とします。

線形予測子: 1次線形結合
リンク関数: ロジット関数
確率分布: ベルヌーイ分布

数式で表現すると以下となります。
$$ \log \frac{p_i}{1-p_i} = X \cdot \beta $$
$$ Y_i \sim Bernouli(p_i) $$
上記のStanコードを記述し、PyStanを実行します。

import pystan

# 一般化線形モデル
glm = """
data{ 
  int N;
  int K;
  int Y[N];
  matrix[N, K] X;
}

parameters{
  vector[K] b;
}

model{
  vector[N] p = X * b;
  Y ~ bernoulli_logit(p);
}
"""
fit = pystan.stan(model_code=glm, data={'N': N, 'K': K, 'Y': Y, 'X': X}, warmup=1000, iter=2000, chains=4)

PyStanの実行には少し時間がかかります。
モデリング結果は以下となります。
INPUT:

print(fit)

OUTPUT:

Inference for Stan model: anon_model_761a478f1c9b45406c71aeb93621ae8e.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

       mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
b[1]  -0.14    0.01   0.55  -1.16  -0.52  -0.15   0.23   0.93   2519    1.0
b[2]  -0.23  8.0e-4   0.03  -0.29  -0.25  -0.23  -0.21  -0.17   1532    1.0
b[3] -382.6    2.95 124.97 -624.9 -466.8 -383.1 -295.8 -135.4   1794    1.0
b[4]  110.8    0.68  26.13  66.55  92.27 108.64 127.51 167.26   1464    1.0
b[5]  -8.47    0.68  36.38 -86.12 -30.96  -6.79  15.84  59.24   2876    1.0
b[6] 732.07    4.87 226.53 301.16 580.38  726.4 877.75 1187.0   2166    1.0
b[7] -30.08    0.13   4.14  -38.8 -32.82 -29.91 -27.14 -22.58    986    1.0
b[8]  13.23    0.05   1.74  10.11  11.98  13.17  14.38  16.79   1109    1.0
lp__ -65.03    0.06   2.09 -69.99  -66.1 -64.68 -63.54  -62.0   1369    1.0

Samples were drawn using NUTS at Sat Jan 16 03:42:16 2021.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Rhatが1.1未満なので収束は問題がなさそうです。
最後にパラメータのMCMCサンプルの分布を確認します。

import arviz

arviz.plot_trace(fit)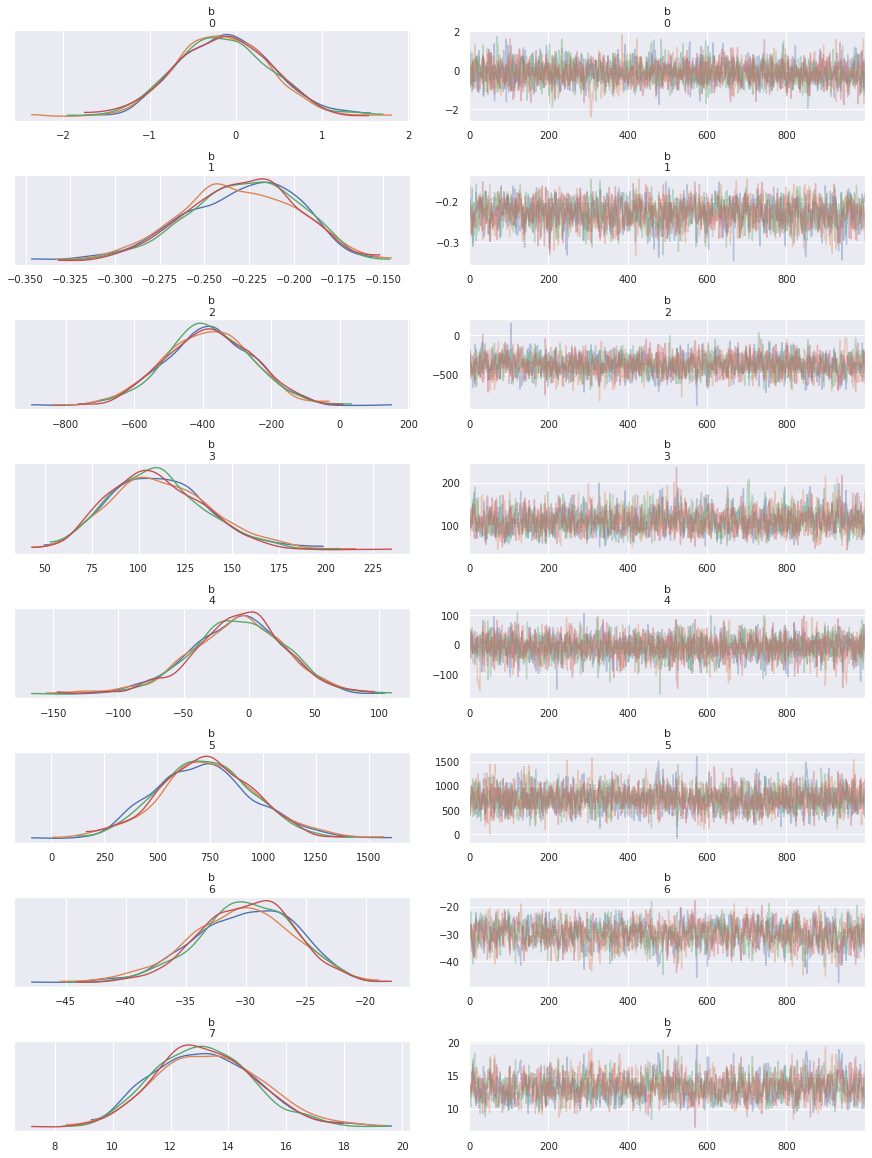

デザイン行列でdataブロックを記述したためパラメータが配列表記になっています。
b[0](texture erro)とb[4](symmetry error)についてはサンプリングで0が含まれるため、これらの変数はベイズ推論の枠組みにおいては肺ガンの良性悪性に寄与しないと言えそうです。

一般化線形混合モデル(GLMM)

最後に一般化線形混合モデル(GLMM)でパラメータを推定します。

GLMMは平均値に応じて分散が増大していく(過分散が生じる)、ポアソン分布などにしたがうデータに対するモデリング手法になります。
ポアソン分布は平均と分散が等しい確率分布です。平均が増加すれば分散も増加します。

なお、ベルヌーイ分布に従う確率変数については過分散の概念は存在しないので、良性か否かを目的変数とするこのデータセットに対してGLMMでモデリングするのは無意味です。

With respect to binomial random variables, the concept of overdispersion makes sense only if n>1 (i.e. overdispersion is nonsensical for Bernoulli random variables).
出典: https://en.wikipedia.org/wiki/Overdispersion

なので、今回はあくまでGLMMでモデリングをやってみるという建て付けでこの章を書いています。

個人ごとに観測値に誤差が存在する想定して、個人単位に正規分布に従うランダム効果を付与することにします。

dataブロックに入力するデザイン行列、目的変数、行列・ベクトルサイズはGLMの場合と同様です。

一般化線形混合モデルで指定する線形予測子、リンク関数、確率分布はそれぞれ以下とします。

線形予測子: 1次線形結合 + ランダム切片(平均 $0$ 、標準偏差 $\sigma$ の正規分布に従う)
リンク関数: ロジット関数
確率分布: ベルヌーイ分布

数式で表現すると以下となります。
$$ \log \frac{p_i}{1-p_i} = X \cdot \beta + r_i $$
$$ r_i \sim N(0, \sigma^2) $$
$$ Y_i \sim Bernouli(p_i) $$
上記のStanコードを記述し、PyStanを実行します。

# 一般化線形混合モデル
glmm = """
data{
  int N;
  int K;
  int Y[N];
  matrix[N, K] X;
}

parameters{
  vector[K] b;
  vector[N] r;
  real sigma;
}

transformed parameters{
  vector[N] p = X * b + r;
}

model{ 
  r ~ normal(0, sigma);
  Y ~ bernoulli_logit(p);
}
"""
fit_glmm = pystan.stan(model_code=glmm, data={'N': N, 'K': K, 'Y': Y, 'X': X}, warmup=1000, iter=2000, chains=4)

PyStanの実行には少し時間がかかります。
PyStan実行完了後、モデリング結果を確認します。

# 表示するパラメータをランダム効果が従う正規分布の標準偏差sigmaと係数ベクトルに限定する
print(fit_glmm.stansummary(pars=['b', 'sigma']))

Inference for Stan model: anon_model_baf824ebc8a4da7810996238f5cd4276.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

        mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
b[1]   26.59   18.14   83.9 -137.4 -18.96  12.82  72.36 219.97     21   1.16
b[2]  -33.65    11.3  19.29 -70.25 -48.92 -32.63 -14.85  -0.45      3   2.98
b[3]  -6.3e4   2.1e4  4.1e4 -1.5e5 -9.0e4 -5.8e4 -2.9e4 -829.2      4   1.93
b[4]   1.6e4  5489.3  1.0e4 201.41 7315.2  1.5e4  2.3e4  3.8e4      3   2.29
b[5]   -1985  1133.2 6080.8 -1.6e4  -5191 -713.2 1199.0 9631.5     29   1.18
b[6]   1.0e5   3.3e4  6.4e4 1430.0  4.8e4  1.0e5  1.4e5  2.4e5      4   1.76
b[7]   -4354  1486.1 2530.6  -8950  -6528  -4096  -2321 -59.47      3   2.95
b[8]  1946.8  663.07 1125.5  25.62 983.73 1853.2 2950.9 3893.2      3   3.11
sigma 275.96   94.89  157.2   2.96 144.51 255.45 410.32 535.41      3   3.72

Samples were drawn using NUTS at Sat Jan 16 04:39:17 2021.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Rhatが1.1未満になっておらず、収束しているとは言えません。
最後にパラメータのMCMCサンプルの分布を確認します。

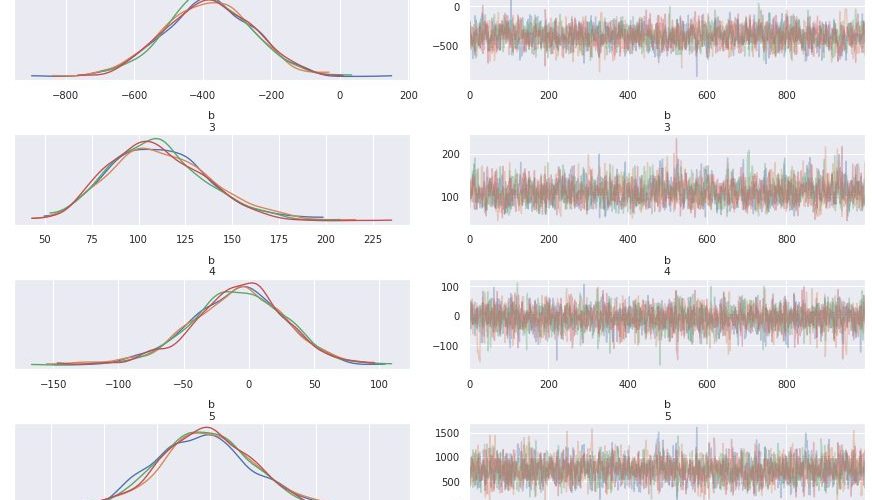
arviz.plot_trace(fit_glmm, var_names=('b', 'sigma'))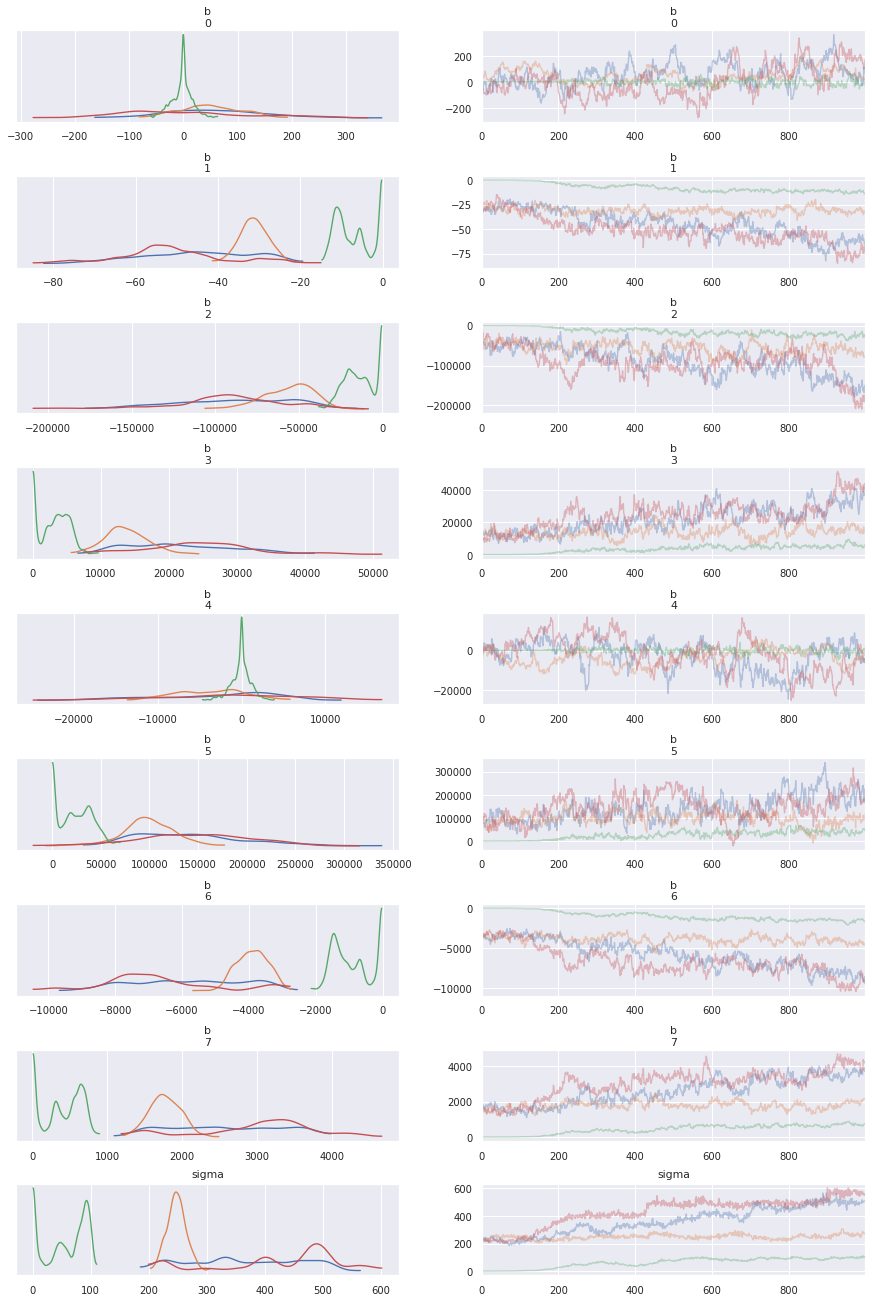

Rhatが1.1より大きいため、MCMCサンプルの分布はめちゃくちゃになっています。

最後に

今回は肺ガンデータセットに対して、一般化線形モデル(GLM)、一般化線形混合モデル(GLMM)を使って分析してみました。
GLMMは本来、目的変数がポアソン分布にしたがっているなどの過分散が疑われるデータ構造に対して適用されるので、今回のようなベルヌーイ分布に従うデータ構造に対してGLMMでモデリングするのは不適当です。
次はGLMMによるモデリングが活かせるデータセットを対象に分析してみようと思います。

参考

前の記事

切片が0の回帰モデルにおける決定係数の解釈 2020.12.21
次の記事

『１分で話せ　世界のトップが絶賛した大事なことだけシンプルに伝える技術』を読んだ感想 2021.01.20