対数変換が適さない場合がある！？対数変換すると結果が悪くなる例の紹介

前回に続き、変数変換のお話です。
KaggleのKernelや諸々のブログで紹介されている手法を見ていて(自分が使う手法も含めて)ふと疑問を感じたことがあってこの記事を書きました。
それは、数値変数(連続値をとる変数)が正規分布に従わない場合に、対数変換によって正規分布に擬似的に従わせたうえでモデルを作っていることです。
正規分布に従わない連続値を対数変換するとよくわからないけど正規分布に従うと信じていますが、これが当てはまらない例ってなんだろうと思い調べてみました。
以下の論文をもとに説明します。

PubMed Central (PMC)

 

72 Pockets

Log-transformation and its implications for data analysis

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4120293/

The log-transformation is widely used in biomedical and psychosocial research to deal with skewed data. This paper highlights serious problems in this classic approach for dealing with skewed data. Despite the common belief that the log transformation ...

正規分布に従わせるための対数変換

連続値を対象にしたモデルの多くは正規分布を仮定しています。
しかし、現実われわれが直面するデータをみるとわかるように、きれいに正規分布している場合はほとんどないと思います。
とは言うものの、なんとか無理やり正規分布に近似させたい。
そんな場合に対数変換が用いられます。

もし、もとのデータが対数正規分布にしたがっているならば、対数変換後のデータは正規分布に従います。
この場合、対数変換によってデータの歪度を取り除くことができたと言えます。
しかし、あるケースにおいては対数変換によって、もとのデータの分布がより歪んでしまう場合もあります。
以下の式で表される \( x_{i} \) の分布を考えます。
$$ x_{i} = 100 \times \left( e^{\mu_{i}} – 1 \right) + 1 $$
ただし、 \( \mu_{i} \sim U(0,1) \) とし、 \( \mu_{i} \) は0から1の一様分布に従うとします。
\( n =10000 \)としたときの \( x_{i} \) を打点し、分布を確かめます。
input:

import numpy as np
import seaborn as sns
import matplotlib as plt
%matplotlib inline

uni = np.random.uniform(0,1,10000) # (0,1)の一様乱数を10,000個生成
x = 100 * (np.exp(uni)-1)+1 #x_iを算出
x = pd.DataFrame(x)
sns.distplot(x, bins=10) #分布をグラフ化
print('the skewness of orginal values is : {}'.format(x[0].skew())) #歪度

skewness is : 0.3555332544813375

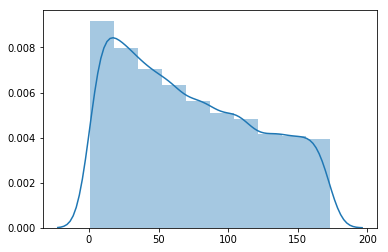
歪度が1を超えており、この分布は正規分布に従っているとは言えません。
さて、この連続値に対して対数変換によって正規分布に近似できるかを確かめます。
\( y_{i} \) は \( x_{i} \) を以下のように対数変換した変数です。
$$ y_{i} = \log (x_{i}) $$
同じく \( n =10000 \) としたときの \( y_{i} \) の分布を確かめます。
input:

y = np.log(x) #xを対数変換
y = pd.DataFrame(y)
sns.distplot(y, bins=10) #分布をグラフ化
print('the skewness of log-transformed values is : {}'.format(y[0].skew())) #歪度

output:

the skewness of log-transformed values is : -1.1508887554091043

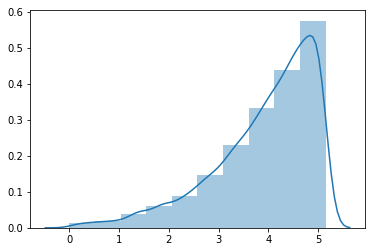
かなり右に裾野が伸びていて、 \( x_{i} \) と同様に正規分布に従うとは言えなさそうです。
さらに歪度を比較すると、 \( x_{i} \) よりも \( y_{i} \) の方が絶対値が大きく、対数変換によってより分布が歪む結果となりました。

もし、もとのデータが対数正規分布に従がっているのであれば、対数変換により正規分布に近似できます。
しかし、もとのデータが対数正規分布に従っていない場合は、対数変換によりさらに歪度が増大し、正規分布から離れてしまうのです。

分散を減少させるための対数変換

対数変換はデータを正規分布に従わせる以外にも、外れ値が含まれるデータの分散を小さくするためにも使われます。
しかし、ケースによっては対数変換によって分散が増大してしまうこともあります。

以下で表される \( y_{i} \) の分散を考えます。
$$ y_{i} = \beta_{0} + \epsilon_{i} $$
ただし、 \( \beta_{0} \) は定数で、 \( \epsilon_{i} \sim U(-0.5,0.5) \) とし、 \( \epsilon_{i} \) は-0.5から0.5の一様分布に従うとします。
ここで \( n=100 \) 回 \( y_i \) をサンプリングし、もとの \( y_{i} \) と対数変換の \( \log y_{i} \) に最小二乗法を適用し、標準誤差 \( \sigma \) を求めます。

ここで標準誤差の推定で偏りを小さくするため、1,000回モンテカルロシミュレーションをします。
input:

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# 変数宣言
n = 100 #MCシミュレーション数
std_origin_ = [] #シミュレーションごとのSTD
std_log_ = [] #シミュレーションごとのSTD
std_origin = [] #betaごとのSTD
std_log = [] #betaごとのSTD
b = [] #beta

# betaを0.5から0.1刻みでloop
for b0 in np.arange(0.5,5.0,0.1):
    # MCシミュレーションloop
    for i in range(n):
        # -0.5〜0.5の一様乱数ベクトルe生成
        e = np.random.uniform(-0.5,0.5,100) # (-0.5,0.5)の一様乱数を100個生成
        # y  = beta_0 + e
        y = b0 + e
        # 標準偏差算出
        std_origin_.append(np.std(np.mean(y)-y))
        std_log_.append(np.std(np.mean(np.log(y))-np.log(y)))
    # 標準偏差算出
    std_origin.append(np.mean(std_origin_))
    std_log.append(np.mean(std_log_))
    b.append(b0)

# beta、もとモデルのSTD、対数変換後のモデルのSTDをデータフレーム変換
data = pd.DataFrame(
    [
        b
        , std_origin
        , std_log
    ]
).T
# ベータごとの標準偏差をグラフ化
plt.plot(data[0],data[1])
plt.plot(data[0],data[2])
plt.ylim([0,1])
plt.xlabel('beta')
plt.ylabel('standard deviation')
plt.show()

output: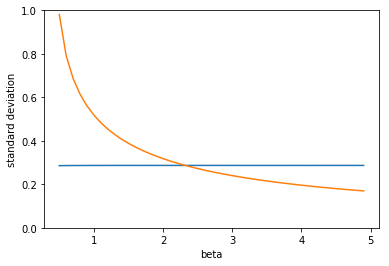

\( \beta \) が小さいときは元のモデルの方が標準誤差が小さいですが、 \( \beta \) が2を超えたあたりから対数変換後の方が標準偏差が小さくなります。

次に6,4,8,10という外れ値を加えた場合の、もとのモデルと対数変換後のモデルの標準偏差を比較する。
input:

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# 変数宣言
n = 100 #MCシミュレーション数
std_origin_ = [] #シミュレーションごとのSTD
std_log_ = [] #シミュレーションごとのSTD
std_origin = [] #betaごとのSTD
std_log = [] #betaごとのSTD
b = [] #beta

# betaを0.5から0.1刻みでloop
for b0 in np.arange(0.5,5.0,0.1):
    # MCシミュレーションloop
    for i in range(n):
        # -0.5〜0.5の一様乱数ベクトルe生成
        e = np.random.uniform(-0.5,0.5,100) # (-0.5,0.5)の一様乱数を100個生成
        # y  = beta_0 + e
        y = b0 + e
        # 外れ値の追加
        np.append(y,[4,6,8,10])
        # 標準偏差算出
        std_origin_.append(np.std(np.mean(y)-y))
        std_log_.append(np.std(np.mean(np.log(y))-np.log(y)))
    # 標準偏差算出
    std_origin.append(np.mean(std_origin_))
    std_log.append(np.mean(std_log_))
    b.append(b0)

# beta、もとモデルのSTD、対数変換後のモデルのSTDをデータフレーム変換
data_ = pd.DataFrame(
    [
        b
        , std_origin
        , std_log
    ]
).T

# 外れ値がない場合とある場合との比較
plt.subplot(1,2,1)
# ベータごとの標準偏差をグラフ化
plt.plot(data[0],data[1],label='original')
plt.plot(data[0],data[2],label='log-transformed')
plt.ylim([0,1])
plt.xlabel('beta')
plt.ylabel('standard deviation')
plt.title('without outlier')
plt.legend()

plt.subplot(1,2,2)
# ベータごとの標準偏差をグラフ化
plt.plot(data_[0],data_[1],label='original')
plt.plot(data_[0],data_[2],label='log-transformed')
plt.ylim([0,1])
plt.xlabel('beta')
plt.ylabel('standard deviation')
plt.title('with outlier')
plt.legend()
plt.tight_layout()

output: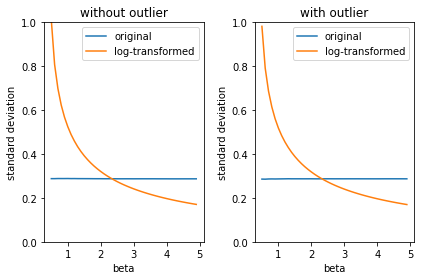

外れ値の有無に関わらず、ほぼ同一の挙動をしていると言えそうです。
\( \beta \) が大きい、つまり平均値が大きい場合は対数変換によって分散(標準偏差)が小さくなり、 \( \beta \) が小さい、つまり平均値が小さい場合は対数変換は分散を増大させています。

まとめ

今まで見てきたように、場合によっては対数変換をしても正規分布に従わなかったり(歪度を減少させる)、分散が増大したりするケースがあることがわかりました。
Pythonで実装するならnumpyのlog1p()、log()メソッドなど
とは言え、対数変換はお手軽に実装できるので、まずは対数変換を試してみるという手は間違いではないでしょう。
重要なのは、対数変換でもうまくいかない場合があることを知っておくことだと思います。