タイタニック号の乗客の生存予測〜誰でも理解できる予測モデルの構築

明けましておめでとうございます。
今年初投稿です。
明日からいよいよ仕事が始まりますね。
今年の抱負は「できない理由ではなく、できる方法を探す!」です。
仕事でも趣味でも、新しい分野にどんどんチャレンジして、スキルや知見を貯めていかねば。
さて、今回はまたタイタニック号の乗客の生存予測に関してです。
前から投稿している内容とは異なり、中学数学レベルの内容で誰にでもわかるようなモデルを作って予測してみます。
※タイタニック号の乗客の生存予測の詳細はこちら
今流行りの機械学習に任せればブラックボックス的に生存予測ができてしまいますが、なぜその予測結果となったのかを説明することは非常に困難です。
この説明の困難さは、ビジネスの意思決定の現場では結構曲者です。
そこで、今回は機械学習などの高度な手法を一切使わずに、誰でも容易に理解できる、ホワイトボックス的な乗客の生存予測モデルを作ってみます。
最も単純な予測モデル
最も単純なモデルとはズバリ。
全ての乗客が生存
乗客の生存確率が50%だった場合を考えてみましょう。
このとき、「最も単純なモデル」を当てはめると、半分の乗客の生存を的中できたことになるので、予測精度は50%となりますね。
しかし、このモデルは実際には全くあてにならないことがわかっています。
wikipediaによると、タイタニック号の乗客の生存率はおよそ33%(2,224人中、約1,500人死亡)です。
当時最大の客船であったタイタニック号は、1912年4月14日の23時40分(事故現場時間)に氷山に衝突した時には2,224人を乗せていた。事故が起きてから2時間40分後の翌4月15日の2時20分に沈没し、1,500人以上が亡くなった。
wikipediaより
このデータを正しいものと仮定して、先ほどの「最も単純なモデル」を当てはめてみましょう。
このとき、全乗客のうちの33%の生存を的中できたことになるので、その予測精度は33%となってしまいます。
このような事前情報のもとでは、以下のモデルにすべきだと検討がつくでしょう。
全ての乗客が死亡
このモデルを使えば、実際の生存率は33%(つまり死亡率は67%)なので、67%の乗客については死亡を予測できたことになります。
つまり、この「最も単純なモデル・改」では、67%もの予測精度が得られることになるのです。
生存予測に使えそうな変数
さすがに「最も単純なモデル・改」では予測モデルが大雑把すぎるので、もう少し踏み込んでみます。
まずは、生存にどの変数が強く相関しているかを確認します。
ちなみに今回はわかりやすいモデル作成のため、カテゴリカル変数(Survived(生存)、Sex(性別)、Pclass(階級)、Embarked(乗船した港))のみにマトを絞っています。
以下、Pythonを使って解析しています。
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
# 学習データの読み込み
train = pd.read_csv('input/train.csv')
# カテゴリカル変数のみ抽出
train_cat = train[['Survived','Pclass','Sex','Embarked']]
# 欠損値の除外
train_cat_null_omit = train_cat.dropna()
# カテゴリカル変数を数値変換
label = LabelEncoder()
train_cat_null_omit['Sex_Code'] = label.fit_transform(train_cat_null_omit['Sex'])
train_cat_null_omit['Embarked_Code'] = label.fit_transform(train_cat_null_omit['Embarked'])
# 相関行列のヒートマップ
heatmap = sns.heatmap(train_cat_null_omit.corr(),cbar=True,annot=True,square=True)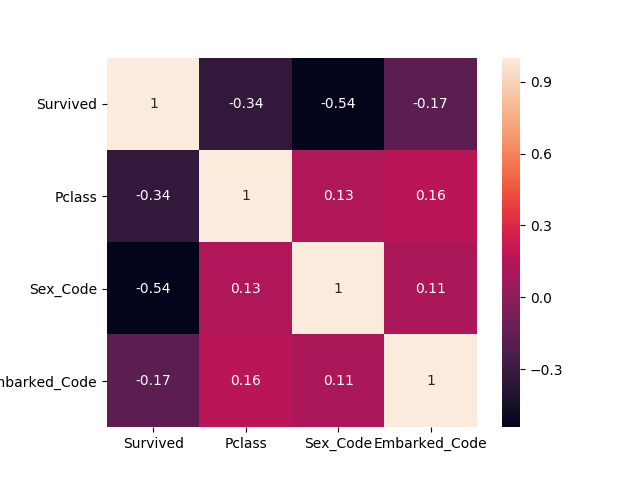
Survived(生存)との相関関係は、Sex(性別) > Pclass(階級) > Embarked(乗船した港)の順になっていることが確認できました。
「最も単純なモデル・改」に、「性別」、「階級」、「乗船した港」の観点を入れた方が予測精度の高いモデルになりそうですね。
以降は、「性別」、「性別×階級」、「性別×階級×乗船した港」の順にモデルを深掘りしていきます。
男は死んで、女は生きるモデル
ではSurvived(生存)を、Sex(性別)の観点からみてみましょう。
# 棒グラフ(性別と生存率)
sns.barplot(x = 'Sex', y = 'Survived', data=train_cat_null_omit)
train_cat_null_omit.groupby('Sex')['Survived'].agg([np.mean,np.size])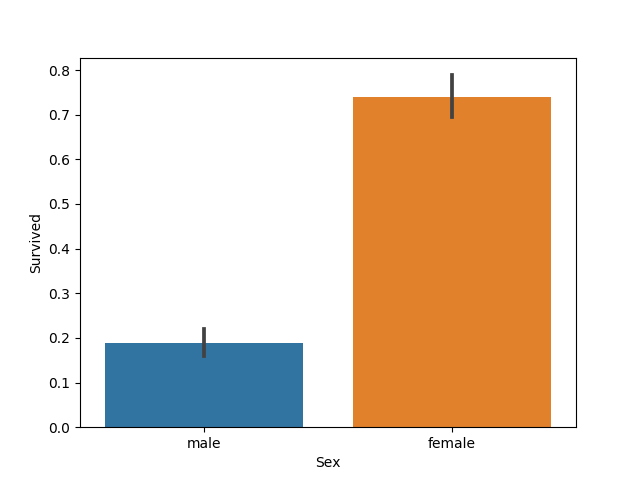
Out[49]:
mean size
Sex
female 0.740385 312
male 0.188908 577女性は74%の確率で生存し、男性は19%の確率で生存(81%の確率で死亡)したということがわかります。
「最も単純なモデル・改」を当てはめると、女性は74%の予測精度になりますが、反面、男性の予測精度は19%となってしまいますね。
そこで、以下のようなモデルを構築します。
・女性は生存
・男性は死亡
このとき、女性の予測精度は74%、男性の予測精度は81%となりますね。
全体での予測精度は以下により計算できます。
$$ \frac{0.740385 \times 312+(1-0.188908) \times 577}{312+577} = 0.786 $$
したがって、この「男は死んで、女は生きるモデル」にしただけで予測精度は79%となるのです。
性別×階級でみた生存
性別と階級との組み合わせが、どう生存に関係してくるのかを確認します。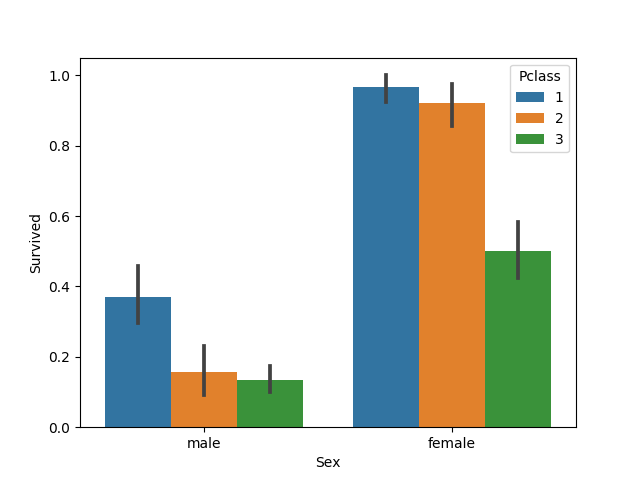
mean size
Sex Pclass
female 1 0.967391 92
2 0.921053 76
3 0.500000 144
male 1 0.368852 122
2 0.157407 108
3 0.135447 347女性、男性で観点を分けてみていきましょう。
女性の乗客
「男は死んで、女は生きるモデル」で、既に女性は全員生存することになっています。
なので、女性の乗客のうちの一部が死亡するモデルを作ることで、予測精度の向上を狙います。
結果をみると、階級が1、2の乗客は生存率が90%を超えているので、モデル変更(生存から死亡へ)の余地はありません。
ただし、階級が3(低いグレード)の乗客は生存率が50%となっており、まだ深掘りすることで生存率が低い項目を発見できる可能性があります。
男性の乗客
「男は死んで、女は生きるモデル」で既に男性は全員死亡することになっています。
なので、女性とは逆で、男性の乗客のうちの一部が生存するモデルを作ることで、予測精度の向上を狙います。
結果をみると、どの階級でも生存率が低く(50%を下回っているため)、モデル変更(死亡から生存へ)の余地はありません。
なので、男性乗客に関してはこれ以上の深掘りは無意味と言えます。
女性で階級が低い乗客のうち、ある港からの乗客は死亡
女性で階級が3(低いグレード)の乗客について、Embarked(乗船した港)の観点でみてみましょう。
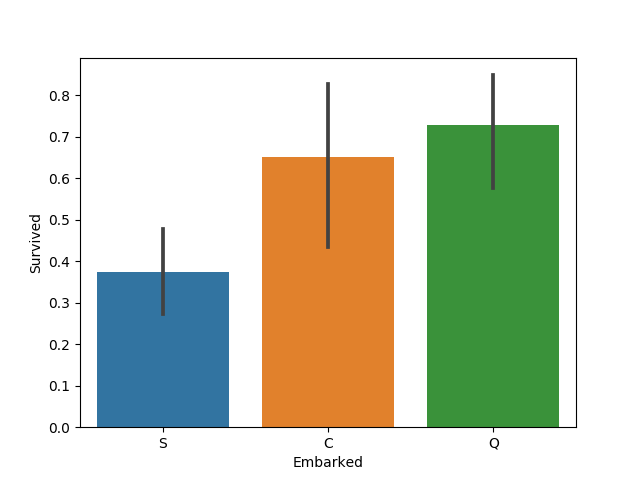
mean size
Embarked
C 0.652174 23
Q 0.727273 33
S 0.375000 88「男は死んで、女は生きるモデル」では女性は全員生存としているので、生存率が50%を下回っているEmbarked(乗船した港)がないかを探します。
結果をみると、S(Southampton)で乗船した女性乗客の生存率が50%を下回っていることがわかります。
つまり、女性で階級が3の乗客のうち、S(Southampton)で乗船した場合は死亡するとした方が良いですね。
したがって、「男は死んで、女は生きるモデル」に以下のルールを追加することで精度が向上されます。
全体的なモデルの精度
最終的なモデルは以下となります。
・男性は死亡
・女性のうち
ー階級3の乗客でS(Southampton)から乗った乗客は死亡
ーそれ以外は生存
かなりシンプルで分かりやすいモデルですね。
しかも、計算は省略しますが、予測精度は81%です。
案外、今回のようにハンドメイドで決定木を作って予測してみるのもアリなのかもしれませんね。
学習用データのみの予想精度なので、あてにはなりません。。。
一度この予測モデルでsubmitしてみましょうか。
- 前の記事

『アルゴリズム思考術:問題解決の最強ツール』を読んだ感想 2017.12.29
- 次の記事

『いまさら聞けない ビットコインとブロックチェーン』を読んだ感想 2018.01.22