現場で使える！2つのグループにおける比率差の検定

今回はPDCAサイクルの検証フェーズで良く用いられる、統計的仮説検定、特に比率の検定について投稿します。

比率の検定は、DM開封率や視聴率などの指標を、KPIに設定している場合に使います。

統計的仮説検定が使われる理由、それは、料金設定や広告、PR活動などのマーケティング施策が、その指標に影響を与えているかどうかを数学的に検証できるからです。

施策実施の前後で、DM開封率や視聴率などの指標に差があった場合、その差が偶然によって生じたものかどうか、明確なエビデンスを与えることができます。

次に当てはまる方は、「統計的仮説検定とは」と「【実践編】DM開封率における差の検証」だけをご覧ください。

統計的仮説検定とは

統計的仮説検定とはズバリ。

ある仮説を立て、その仮説をもとに検証した結果に応じて、仮説を採択したり、棄却したりすることです。

高校数学で習う、背理法の概念に似ていますね。

ちなみに、背理法は、わざと否定されるであろう仮定を立てて、論証の末に仮定が否定されることを証明する方法でしたね。

統計的仮説検定も背理法と同様に、わざと棄却されそうな仮説を立てるのです。

（統計的仮説検定では、否定ではなく棄却というワードを用います。）

これを帰無仮説といいます。

読んで字のごとく、無に帰される仮説です。

帰無仮説を立てたうえで、検定統計量と呼ばれる、検定の基準となる数値を算出します。

検定統計量の数値によって、帰無仮説の採択、棄却を行います。

【理論編①】母比率の検定

母比率の検定とは

まわり道だと思うかもしれませんが、まずは母比率の検定を解説します。

2つのグループにおける比率差の検定を理解するためには、これを理解しておく必要があるからです。

母比率の検定とはズバリ。

観測した標本比率 \( p_{0} \) が、母比率 \( p \) と有意差がないかを検証することです。

例えば、こんなときに使います。

この例の場合、標本比率 \( p_{0} = 0.70 \) で、母比率 \( p=0.50 \) となります。

検定統計量の導出

確率変数 \( X \) がベルヌーイ分布 \( Bi(1,p)\) に従うとします。

$$ X \sim Bi(1,p) \tag{1} $$

このとき、平均 \( E[X] \) 、分散 \( Var[X] \) について以下が成立します。

\begin{eqnarray}
E[X] &=& 1 \times p + 0 \times (1-p) \\
&=& p \tag{2}
\end{eqnarray}

\begin{eqnarray}
Var[X] &=& E[X^2]-(E[X])^2 \\
&=& p(1-p) \tag{3}
\end{eqnarray}

次に、標本平均 \( \overline{X} \)についての平均、分散を求めます。

\begin{eqnarray}
E\left[ \overline{X} \right] &=& E\left[ \frac{X_{1}+X_{2}+\cdots+X_{n}}{n} \right] \\
&=& E\left[ \frac{1}{n}\sum^{n}_{i=1}X_{i} \right] \\
&=& \frac{1}{n} E\left[ \sum^{n}_{i=1}X_{i} \right] \\
&=& p \tag{4}
\end{eqnarray}

\begin{eqnarray}
Var\left[ \overline{X} \right] &=& Var \left[ \frac{1}{n}\sum^{n}_{i=1}X_{i} \right] \\
&=& \frac{1}{n^2} Var\left[ \sum^{n}_{i=1}X_{i} \right] \\
&=& \frac{1}{n^2} \sum^{n}_{i=1} Var[ X_{i} ] \\
&=& \frac{p(1-p)}{n} \tag{5}
\end{eqnarray}

ここで、 \( n \) が十分大きいとき、中心極限定理により、標本平均 \( \overline{X} \) は正規分布 \( N(p,p(1-p)/n) \) に近似できます。

$$ \overline{X} \sim N\left( p,\frac{p(1-p)}{n} \right) \tag{6} $$

この正規分布 \( N(p,p(1-p)/n) \) を以下の \( Z \) によって標準化します。

$$ Z = \frac{\overline{X}-p}{\sqrt{p(1-p)/n}} \tag{7} $$

ここで、標本平均 \( \overline{X} \) については以下が成立します。

$$ \overline{X} = \frac{1}{n}\sum^{n}_{i=1}X_{i} = p_{0} \tag{8} $$

（ \( p_{0} \) は標本比率であり、母比率 \( p \) とは異なります。 ）

(7)式に(8)式を代入し、最終的に以下の\( Z \) を得ます。

$$ Z = \frac{p-p_{0}}{\sqrt{p(1-p)/n}} \tag{9} $$

この\( Z \) は標準正規分布 \( N(0,1) \) に従います。

これで検定統計量の導入は完了です。

検定実施

標本比率を \( p_{0} \) ，母比率を \( p \) とすると、帰無仮説 \( H_{0} \)は以下となります。

$$ H_{0}\;:\;p_{0}=p $$

検定統計量 \( Z \) が棄却域に入るとき、帰無仮説は棄却され、標本比率と母比率の間には有意差があることになります。

ここでは、有意水準 \( \alpha = 0.05 \) とし、両側検定としています。

統計解析言語Rを使って、帰無仮説の棄却域を描画しました。
サンプルコードは以下になります。

lower_reject <- qnorm(0.025)
upper_reject <- qnorm(0.025,lower.tail=FALSE)
curve(dnorm(x,mean=0,sd=1),from=-4,to=4,add=TRUE)
abline(v=c(lower_reject,upper_reject))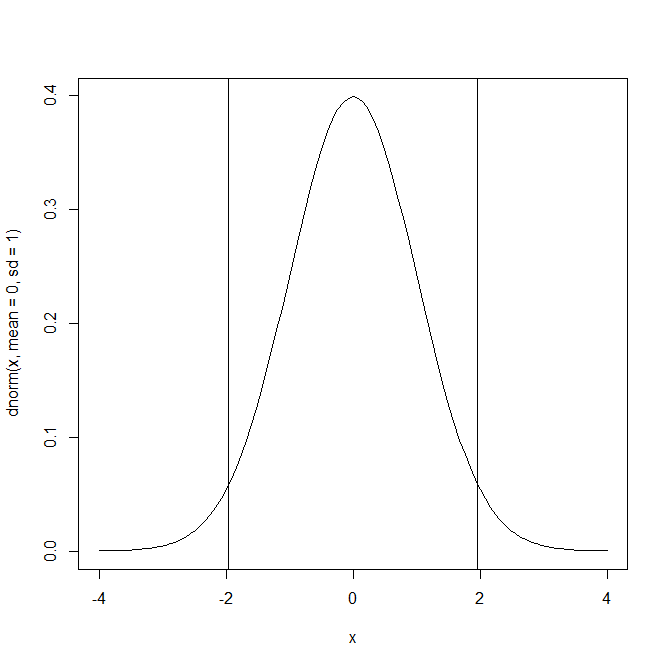

それぞれの縦線から裾野までの領域が棄却域となります。
ここに検定統計量 \( Z \) が入るとき、帰無仮説は棄却されます。
以下のコードで、具体的な棄却域を求めます。

> upper_reject
[1] 1.959964
> lower_reject
[1] -1.959964

従って、 \( |Z| \geq 1.959964 \) を満たすとき、帰無仮説は棄却されます。

【理論編②】2つのグループにおける比率差の検定

2つのグループにおける比率差の検定とは

比率差の検定とはズバリ。

2つのグループ間での標本比率が異なるとき、それが本当に有意な差なのかどうかを検証することです。

例としては、視聴率があげられます。

ある地域では視聴率が3%で、他の地域では視聴率が1%だった場合に、これが偶然による差なのかどうかを数学的に検証できます。

検定統計量の導出

ベルヌーイ分布に従う、以下の2つの確率変数 \( X,\;Y \) を考えます。

$$ X \sim Bi(1,p_{1}),\;\;\;\ Y \sim Bi(1,p_{2}) $$

以下、帰無仮説 \( H_{0}\;:\;p_{1}=p_{2} \) のもとで検定統計量を導出します。

（導出の過程で、 \( p_{1}=p_{2}=p \) とおいています。
帰無仮説により、\( p_{1} \) と \( p_{2} \)は等しいので、それを \( p \)としているだけです。
ちなみにこの \( p \) を加重平均といいます。）

標本比率の差 \( \overline{X}-\overline{Y} \) を対象に平均値、分散を求めます。

\begin{eqnarray}
E\left[ \overline{X}-\overline{Y} \right] &=& E\left[ \overline{X} \right]-E\left[\overline{Y} \right] \\
&=& p-p \\
&=& 0 \tag{10}
\end{eqnarray}

\begin{eqnarray}
Var\left[ \overline{X}-\overline{Y} \right] &=& Var \left[ \overline{X} \right]+Var\left[ \overline{Y} \right] \\
&=& \frac{p(1-p)}{n}+\frac{p(1-p)}{m} \\
&=& p(1-p)\left( \frac{1}{n}+\frac{1}{m} \right) \tag{11}
\end{eqnarray}

\( \overline{X}-\overline{Y} \) は \( n,\;m \) が十分に大きいとき、正規分布 \( N(0,p(1-p)/(1/n+1/m)) \) に近似できます。

\( \overline{X}-\overline{Y} \) を \( Z \) で標準化します。

$$ Z = \frac{ \overline{X}-\overline{Y} }{\sqrt{p(1-p)/(1/n+1/m)}} \tag{12} $$

ここで、\( \overline{X}=p_{sample1},\;\overline{Y}=p_{sample2} \)を(12)式へ代入し、以下の式を得ます。

$$ Z = \frac{ {p}_{sample1}-{p}_{sample2} }{\sqrt{p(1-p)/(1/n+1/m)}} \tag{13} $$

（ \( {p}_{sample1},\;{p}_{sample2} \) は標本比率であり、母比率 \( p_{1},\;p_{2},\;p \) とは異なります。 ）

母比率 \( p \) は以下で推定します。

$$ p = \frac{p_{sample1} \times m + p_{sample2} \times n}{m+n} $$

これで検定統計量の導出が完了です。

検定実施

帰無仮説： \( H_{0}\;:\; p_{1}=p_{2} \) として検定を実施します。

母比率の検定とまったく同様です。

検定統計量 \( Z \) を算出し、棄却域に入るかどうかを検証します。

【実践編】DM開封率における差の検証

ケーススタディ

以下のケースを考えてみましょう。

検定統計量の計算

以下の検定統計量 \( Z \) を算出しましょう。

$$ Z = \frac{p_{sample1}-p_{sample2}}{\sqrt{p(1-p)(1/m+1/n)}} $$

まず \( Z \) の算出に必要な値を整理します。

変更前の標本数 \( m = 1000 \) 、開封率 \( p_{sample1} = 0.30 \)

変更後の標本数 \( n = 3000 \) 、開封率 \( p_{sample2} = 0.32 \)

加重平均 \( p = (p_{sample1}m+p_{sample2}n)/(m+n)=0.315 \)

従って、検定統計量 \( Z \) は以下になります。

$$ Z = \frac{0.30-0.32}{\sqrt{0.315(1-0.315)(1/1000+1/3000)}} $$

よって、 \( Z = -1.17912559 \)

検定実施

有意水準 \( \alpha =0.05 \) とします。

以下の条件を満たしたときに帰無仮説（2つのグループ間に比率の差はない）は棄却されます。

$$ |Z| \geq 1.959964 $$

検定統計量\( Z \)は、 \( -1.17912559 \) であったため、条件を満たしません。

従って、帰無仮説は棄却されないので、標本比率に有意差はないといえます。

もっと正確には、帰無仮説のもとで検証した場合でも、十分に起こりうる確率でこの差が生じていると言えます。