よく使われる2つのスコアの集約関数と複比ユニノルムとの比較

最近、相互推薦システムについて調べていて、Latent Factor Models and Aggregation Operators forCollaborative Filtering in Reciprocal Recommender Systemsという論文を読んでいます。

その中で、2つの選好スコアの集約関数についての記載がありました。ここで、選好スコアとは、ユーザAがユーザBをどれくらい好むのかを表現する数値を指します。ユーザAがユーザBを好むスコアと、逆にユーザBがユーザAを好むスコアを集約することを考えています。
相互推薦システムにおいては、この2つの選好スコアをどう集約するかが重要なのだそうです。

今回はこの2つ選好スコアの集約でよく使われる算術平均、調和平均、幾何平均に加えて、本論文で紹介されているcross rasio uninorm（複比ユニノルム）について、簡単にどういう分布になるのかを比較してみました。

算術平均

あらゆる分野でよく使われる集約関数です。他の集約関数とは異なり、入力した値の大小によって集約結果が偏らないのが特徴的です。
定義は以下です。
$$
M(x_1, x_2) = \frac{x_1+x_2}{2}
$$

実装コードは以下です。

def arithmetic_mean(x, y):
  return (x+y)/2

幾何平均

算術平均とは異なり、集約結果が入力した数値の小さい方に偏るという特徴があります。
定義は以下になります。
$$
G(x_1, x_2) = \sqrt{x_1x_2}
$$

実装コードは以下です。

def geometric_mean(x, y):
  return np.sqrt(x*y)

調和平均

幾何平均と同様に、集約結果が入力した数値の小さい方に偏るという特徴があります。相互推薦システムで一般的に用いられる集約関数とのこと。
定義は以下です。
$$
H(x_1, x_2) = \frac{2x_1x_2}{x_1+x_2}
$$

実装コードは以下です。

def harmonic_mean(x, y):
  return 2*x*y/(x+y)

cross-ratio uninorm(複比ユニノルム)

本論文で紹介されている集約関数です。
上記で挙げた、算術平均、幾何平均、調和平均とは異なり、以下の特徴があります。

• 2つの入力値が低ければ、集約して低い値を生成する（接続）
• 2つの入力値が高ければ、集約して高い値を生成する（分離）
• 入力値の一方が高く、一方が低い場合、集約して両者の間にある値を生成する（平均化）

上記の特徴は、完全強化特性(full reinforcement property)と呼ばれるようです。
定義は以下です。
$$
U(x_1, x_2) = \frac{x_1x_2}{x_1x_2 + (1-x_1)(1-x_2)}
$$

実装コードは以下です。

def cross_rasio_uninorm(x, y):
  return x*y/(x*y+(1-x)*(1-y))

比較結果

数式だけだとイメージにしにくいので、 \((x,y) \in [0,1] \times [0,1]\) に対して上記の集約関数による出力結果を可視化し、どういう分布になるのかを比較してみました。

環境は以下です。

• python: 3.6
• numpy: 1.18.4
• pandas: 1.0.3

import numpy as np
import pandas as pd
from mpl_toolkits.mplot3d import Axes3D

# X:[0,1]×Y:[0,1]のグリッド作成
x = np.arange(0.0, 1.0, 0.1)
y = np.arange(0.0, 1.0, 0.1)
X, Y = np.meshgrid(x, y)

fig = plt.figure(figsize=(15,10))
ax = fig.add_subplot(221, projection='3d')
ax.plot_wireframe(X, Y, arithmetic_mean(X, Y))
ax.set_title("arithmetic mean")

ax = fig.add_subplot(222, projection='3d')
ax.plot_wireframe(X, Y, geometric_mean(X, Y))
ax.set_title("geometric mean")

ax = fig.add_subplot(223, projection='3d')
ax.plot_wireframe(X, Y, harmonic_mean(X, Y))
ax.set_title("harmonic mean")

ax = fig.add_subplot(224, projection='3d')
ax.plot_wireframe(X, Y, cross_rasio_uninorm(X, Y))
ax.set_title("uninorm")

plt.show()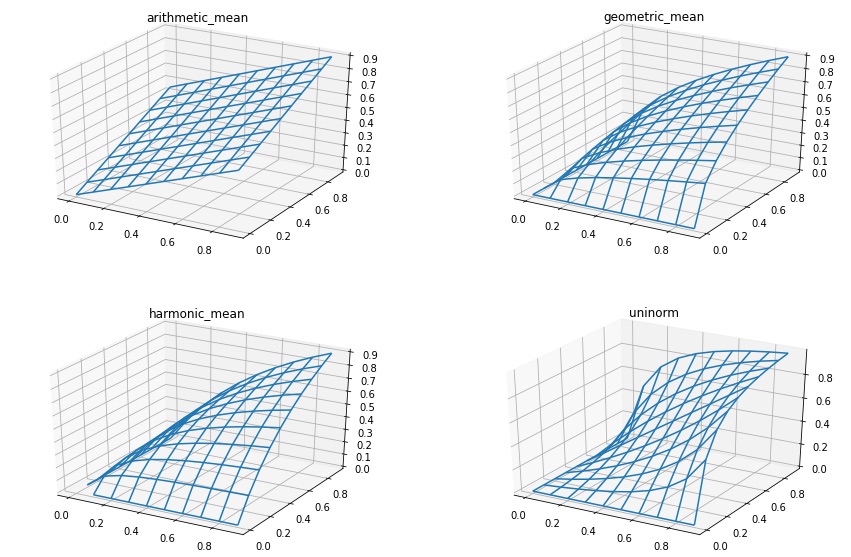

定義通り、算術平均(左上)は線形な分布になっています。また、幾何平均(右上)と調和平均(左下)は非常に似ている分布になっています。
一方、cross-ratio uninorm(複比ユニノルム)(右下)はなかなか歪な分布になっているのが分かります。
cross-ratio uninorm(複比ユニノルム)はその特徴から、入力した値に乖離がある場合は集約結果が低い値になるものの、入力した値の両方がある程度高い値だと集約結果も高い値になるようです。
確かに、相互推薦システムという文脈で考えると、一方向に偏りがある場合よりも、双方向にある程度好意を持っている方が結果として高いスコアになるというのは最もだなと思いました。