パラメータの初期値を指定してOptunaで最適化してみる

OptunaはPFN社が公開しているオープンソースのハイパーパラメータ自動最適化フレームワークです。
最適化したいパラメータの事前分布と目的関数を定義すれば、あとはベイズ最適化を用いて自動的にパラメータを探索してくれます。
(Optunaの一般的な使用方法はこちらの記事が詳しいです。)
ただ、ある程度パラメータについてのドメイン知識があって、最適なパラメータはこのあたりだと検討がついている場合は初期値を固定してみたくなります。
そこで、今回はOptunaの探索パラメータの初期値を固定する方法を紹介し、簡単な実験でパラメータを固定せずに最適化した結果と比較してみます。

準備

今回はGoogle Colaboratoryを利用しました。
次のコマンドでoptunaをインストールすれば、本記事で紹介するコードが動作します。

# optuna=="2.10.0"
!pip install optuna

パラメータを固定する方法

わざわざチューニングする必要もないですが簡単に \(v^2 + w^2 + x^2 + y^2 + z^2\) を目的関数として定義し、これを最小化するようなパラメータ \(v,w,x,y,z \in \mathbb{R}\) を探索します。
最適解は \( v=w=x=y=z=0 \) で最適値は0です。

def objective(trial):
    v = trial.suggest_uniform('v', -10, 10)
    w = trial.suggest_uniform('w', -10, 10)
    x = trial.suggest_uniform('x', -10, 10)
    y = trial.suggest_uniform('y', -10, 10)
    z = trial.suggest_uniform('z', -10, 10)
    score = v ** 2 + w ** 2 + x ** 2 + y ** 2 + z ** 2
    return score

まず、パラメータの事前分布を仮定し、初期値を固定せずに最適化してみます。
パラメータの事前分布は-10から10の連続一様分布 \(v,w,x,y,z \sim U(-10,10) \) とします。

import optuna

study_1 = optuna.create_study()
study_1.optimize(objective, n_trials=100)
print(f'best_params: {study_1.best_params}')
print(f'best_value: {study_1.best_value}')

OUTPUT:

best_params: {'v': 0.01272595124035758, 'w': 0.8694024673605734, 'x': 0.9314747082980765, 'y': -0.8405487040309302, 'z': 4.950198268116601e-05}
best_value: 2.330189858585134

次に、パラメータの初期値を固定して最適化をしてみます。
こちらの記事で初期値を固定する方法がまとめられていましたが、optunaのenqueue_trial()で試行しておきたいパラメータをエンキューするだけでも実装可能です。
今回はenqueue_trial()で実装します。
初期値は \( v=w=x=y=z=1 \) とします。

study_2 = optuna.create_study()
study_2.enqueue_trial({'v': 1, 'w': 1, 'x': 1, 'y': 1, 'z': 1})
study_2.optimize(objective, n_trials=100)
print(f'best_params: {study_2.best_params}')
print(f'best_value: {study_2.best_value}')

OUTPUT:

best_params: {'v': 1.2556752763089818, 'w': -0.24967548556435926, 'x': -0.24329548698748482, 'y': -0.11691506320707346, 'z': -0.5367382968453831}
best_value: 2.0000080729191105

パラメータの初期値を固定した方が最適値が改善されています。
次にtrialごとの結果も見てみます。

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(study_1.trials_dataframe()['number'], study_1.trials_dataframe()['value'], label='without initial values')
ax.plot(study_2.trials_dataframe()['number'], study_2.trials_dataframe()['value'], label='with initial values')
ax.legend()
ax.set_xlabel('number')
ax.set_ylabel('value')
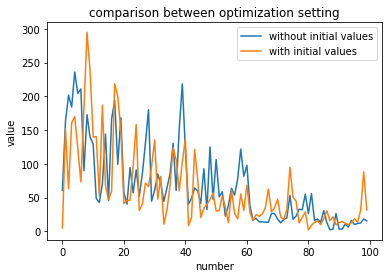
ax.set_title('comparison between optimization setting')

OUTPUT:

青がパラメータの初期値を固定しなかったケース、オレンジがパラメータの初期値を固定したケースです。
このグラフからだとどちらが収束が早いのか、より良い最適値に到達しているのかを判断できません。
また、Optunaではパラメータを確率的にサンプリングしているため、たまたま両者のケースで収束に差が現れなかったのかもしれません。

パラメータの固定有無での最適化結果の比較

確率的なサンプリングによる偶然性を排除するため、上で述べた最適化を100回繰り返し、パラメータの初期値を固定したケースとそうでないケースの最適値の分布を確認してみます。

cnt = list()

for i in range(100):
    study_1 = optuna.create_study()
    study_1.optimize(objective, n_trials=100)

    study_2 = optuna.create_study()
    study_2.enqueue_trial({'v': 1, 'w': 1, 'x': 1, 'y': 1, 'z': 1})
    study_2.optimize(objective, n_trials=100)

    cnt.append((study_1.best_value, study_2.best_value, study_1.best_trial.number, study_2.best_trial.number))

import pandas as pd
import seaborn as sns

df = pd.DataFrame(cnt, columns=['best_value_1', 'best_value_2', 'best_trial_1', 'best_trial_2'])
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
sns.distplot(df['best_value_1'], ax=ax)
sns.distplot(df['best_value_2'], ax=ax)
ax.set_xlabel('best_value')
ax.set_title('distribution of best_value between optimization settings')

OUTPUT: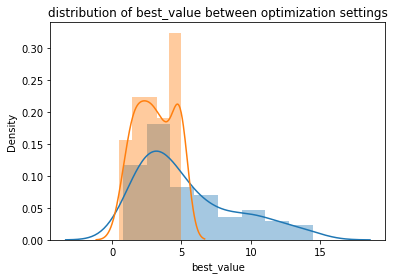

青がパラメータの初期値を固定しなかったケース、オレンジがパラメータの初期値を固定したケースで、横軸は最適値です。
パラメータの初期値を固定したケースでは最適値が5で一つ山がありますが、これは初期値が最適解であったことを示しています。
最適値の分布をみるとパラメータの初期値を固定した方が低い最適値となる場合が多いことが分かります。
したがって、あらかじめパラメータに見当がつく場合は初期値を固定した方が良い最適解を得やすいことが分かりました。